Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 38
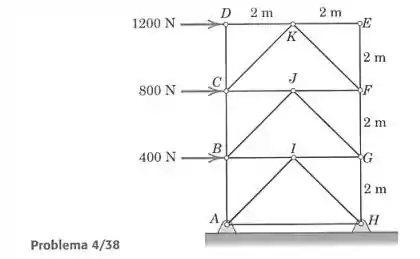
Determine as forças nos elementos e da treliça simétrica carregada. Mostre que esse cálculo pode ser realizado usando uma seção e duas equações, cada uma das quais contendo apenas uma das duas incógnitas. Os resultados são afetados pela indeterminação estáticas dos apoios da base?
Passo 1
Vamos calcular as forças pelo método das seções, partindo a treliça em duas e considerando uma parte dela como se fosse um corpo rígido, e então resolvendo as equações de equilíbrio para esse corpo. Temos interesse nas barras , , e como queremos que nosso cálculo seja com apenas uma seção, o corte que vamos fazer tem que passar nesses dois elementos. Vamos então fazer uma linha passando por , , e :
Pegamos a parte de cima pra evitar as forças desconhecidas na base. A indeterminação estática não afetará nosso cálculo, pois só indetermina a força nas barras e .
Passo 2
Primeiro vamos tentar encontrar . Temos outras três forças desconhecidas, mas queremos uma equação que tenha como incógnita só . As linhas de força de , e passam por então se calcularmos o momento em torno de essas forças não aparecem. Então:
Note que essa força está tracionando o elemento.
Passo 3
Agora usamos a mesma estratégia para calcular . As linhas de força de , e passam por , então essas forças não aparecem no cálculo do momento em torno de :
Note que pelo sentido essa força está comprimindo o elemento
Resposta
A indeterminação estática não afeta o cálculo, pois só indetermina as forças em , e .