Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 2.Problemas - Ex. 1
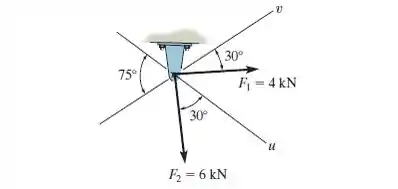
Determine a intensidade da força resultante e sua direção, medida no sentido horário a partir do eixo positivo.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a primeira questão de mais um livro juntos!
Nessa questão nós precisamos calcular a força resultante e o ângulo que forma com a direção do eixo positivo.
A chave desta questão é trabalhar com a geometria do problema. Temos que desenhar no nosso esboço o triângulo de lados dados pelas forças e . A partir das informações obtidas conseguiremos calcular tudo pela lei dos senos.
Então, muito cuidado na hora do esboço!!! Vejamos só ele abaixo:
Na Figura acima, o vetor preto corresponde ao nosso vetor resultante . Para que a gente consiga determinar o nosso ângulo entre a direção positiva do eixo e o vetor , foi necessário definirmos um ângulo .
Este é o ângulo entre os vetores e . Portanto, o nosso ângulo é:
E assim finalizamos as etapas iniciais da nossa questão
Passo 2
Agora que já obtemos o nosso triângulo, basta aplicarmos a lei dos senos para calcular cada um dos vetores decompostos.
Pela lei dos senos nós temos:
Para resolvermos o sistema acima, vamos começar resolvendo a primeira equação, pois só temos uma incógnita. Portanto,
Aplicando a relação de soma de arcos, , temos:
E assim determinamos que o ângulo entre a força resultante e o semi-eixo positivo é:
Passo 3
Para finalizarmos a questão só nos resta definirmos a intensidade da força resultante. Para isto, basta utilizarmos a segunda equação do sistema que montamos no Passo 2. Portanto,
E assim finalizamos a nossa questão!