Enunciado
Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.10 - Ex. 16
O que são vetores de base? Por que utilizar esses vetores?
Passo 1
Eae meus jovens padwans, suave na nave? Espero que sim hehe’. Vamos resolver mais um exercício sobre vetores, e neste caso pergunta o que c@#$% é um vetor de base.
Nem tudo na vida são flores meus mancebos, quando se trabalha em um espaço com mais de uma dimensão, ou melhor, trazendo para a realidade, quando se trabalha com espaço em 3D, é vantajoso utilizar vetores unitários adimensionais segundo os eixos coordenados, denominados vetores cartesianos unitários, vetores unitários de base ou simplesmente vetores de base, que são usualmente denotados por i, j e k.
Passo 2
Fino do fino né senhores? Mas por que usá-los?
Simples, quando se trabalha com grandezas vetoriais, temos que escrever que direção o nosso vetor está indo, porque isso altera significamente se escrevermos errado isso. No caso demonstrado, a base i, j e k é a base cartesiana e temos que indicar o sentido dos vetores nesses planos.
Por exemplo, temos uma força que age em um corpo e ela tem componentes em todas asa direções, ou seja, a força age nas 3 dimensões. Portanto temos que denotar:
Graficamente falando, seria assim, veja:
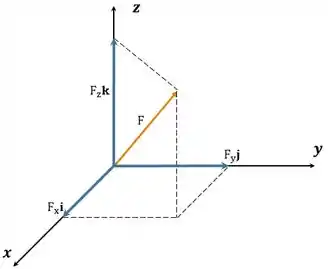
Resposta
São vetores unitários adimensionais segundo os eixos coordenados, denominados vetores de base. Para basicamente indicar o sentido dos vetores nesses planos.