Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 27
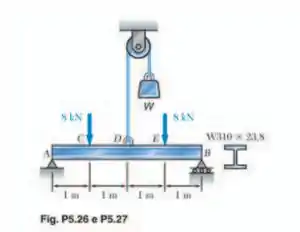
Determine (a) a magnitude do contrapeso para o qual o valor máximo absoluto do momento fletor na viga é o menor possível, (b) a tensão normal máxima correspondente devido à flexão. (Dica: desenhe o diagrama do momento fletor e iguale os valores absolutos do maior momento positivo e negativo obtidos.)
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora praticar mais.
Para resolver o problema, precisamos das reações de apoio em função de . O DCL é:
Para acharmos as reações, vamos utilizar as equações de equilíbrio. Sabemos que:
Por simetria:
O esboço do diagrama de momento é:
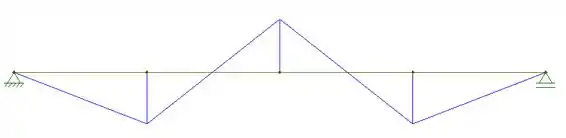
Podemos perceber que o maior valor do momento positivo ocorre em e o maior valor do momento negativo ocorre em Vamos calculá-los e igualá-los. Logo:
E:
Igualando (em módulo):
Passo 2
Determinamos o valor do peso. Agora, vamos substituir os valores e determinar as reações.
Agora, vamos determinar o diagrama para pegar o maior momento atuante.
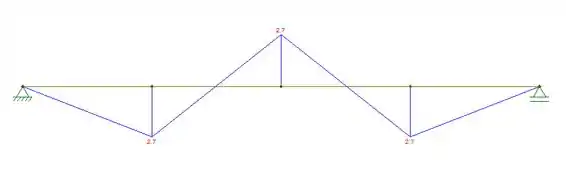
O maior momento é
Sabemos que a tensão é dada por:
Onde é a distância da linha neutra (onde a tensão é nula) até o ponto em que queremos saber a tensão e é o momento de inércia da seção.
Esses valores são tabelados para o perfil indicado, que é o W 310X23,8 Os valores podem ser encontrados em tabelas na internet ou no próprio livro.
Como queremos a máxima tensão, pegaremos o maior Portanto, usando o ábaco:
O momento de inércia também está no ábaco, e é igual a:
Passo 3
Agora, temos todos os dados para obter a tensão normal máximaSubstituindo os valores:
E pronto! Esta é a tensão normal máxima na estruturagerada pelo momento fletor.