Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 89
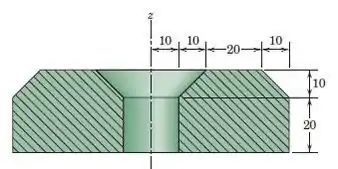
Determine a massa da peça fundida de titânio formada girando completamente a seção transversal mostrada em torno do eixo z de simetria.
Passo 1
Observe que, para determinar a massa da peça fundida, precisaremos determinar seu volume e densidade.
(1)
Na tabela D / 3, vemos que a densidade do titânio é:
Substitua ρ por seu valor na expressão (1) para obter a expressão para a massa (em kg) em função do volume (em mm)
(1.1)
Passo 2
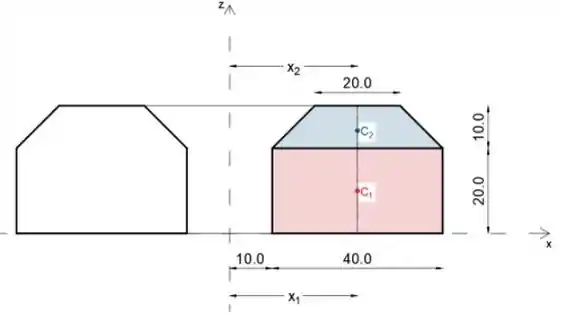
Usando o teorema de Pappus, podemos escrever a expressão para o volume do corpo como
Onde x ‾ é o centroide da área, A é a área e o ângulo de rotação θ
Podemos ver no esboço as seguintes dimensões:
Uma vez que as áreas das partes 1 e 2
E o ângulo de rotação
Passo 3
Coloque os valores na expressão (2)
Volume total é
Finalmente, substitua V pelo seu valor na expressão (1.1) para obter a massa da peça fundida em kg.