Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 146
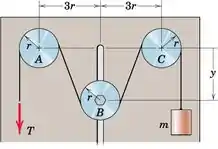
As posições dos eixos A e C são fixas, enquanto as do eixo B podem ser variadas por meio da fenda vertical e do parafuso de travamento. Os coeficientes de atrito cinético são 0,60 em A e C e 0,20 em B. Plote a quantidade T/mg como uma função de y para , onde T é a tensão necessária para levantar o cilindro de massa m em um equilíbrio taxa e r é o raio comum de todos os três eixos. Todos os eixos são fixos contra rotação. Quais são os valores limites de T/mg para y = 0 e para grandes valores de y?
Passo 1
Como estamos tentando levantar o cilindro, sabemos que a tensão T é maior que o peso W, sabendo que o coeficiente de atrito não é igual para todas as superfícies, podemos escrever a expressão para a tensão T como
Desde a
E uma vez que sabemos que W = mg, podemos escrever a expressão acima como
No esboço abaixo, podemos ver que os ângulos , e são
Passo 2
Portanto, a expressão para a tensão T agora será semelhante a esta
A partir daqui, podemos expressar proporção como
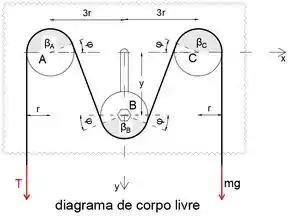
Passo 3
Podemos notar que os triângulos ADE e BEF são idênticos, portanto, podemos escrever a expressão para comprimento como
Em seguida, usando a regra do seno, podemos determinar o ângulo
Uma vez que o intervalo de y é , podemos escrever a equação acima como
Mas agora o intervalo de y é de 0 a 10 (sem r), podemos escrever o ângulo como
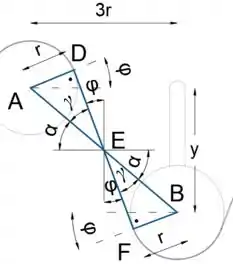
Passo 4
Observe que é o ângulo que a linha AB faz com a horizontal
Enquanto é o ângulo que a linha DF faz com a vertical, portanto, podemos escrever
A partir daqui, podemos expressar o ângulo como
Vamos substituir e pelas expressões (3) e (2), respectivamente
Finalmente, vamos substituir pela expressão (4) na equação (1)
Passo 5
Usando uma calculadora gráfica como o Desmos (link nos comentários), traçaremos esta função
O valor para y = 0
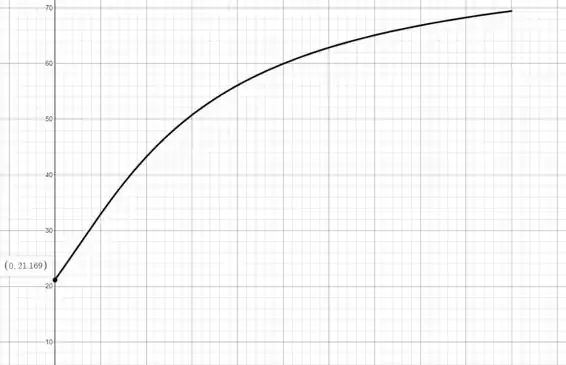
Quando
Portanto, podemos escrever a expressão para quando é