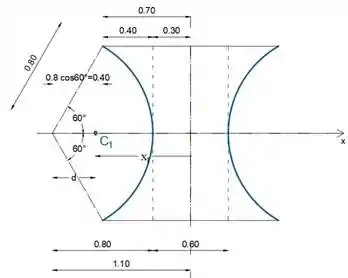
Uma superfície é gerada girando o arco circular de 0,8 m de raio e ângulo subtendido de 120∘ completamente em torno do eixo z. O diâmetro do pescoço é de 0,6 m. Determine a área externa A gerada.

Usando o teorema de Pappus, podemos escrever a expressão para a área do corpo como

Onde x é o centróide das linhas, L é o comprimento das linhas e θ ângulo de rotação

Observe que a distância d do centro do arco até seu centroide é:

Portanto, a distância do centroide C1 ao eixo z é:

E o comprimento do arco é

Uma vez que o ângulo de rotação é