Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 104
Calcule a força de apoio RA e o momento MA atuando na viga cantilever carregada em A.
Passo 1
Primeiro, vamos isolar e desenhar o diagrama de corpo livre da viga
Observe que substituímos a carga distribuída por sua resultante que atua no centro do triângulo
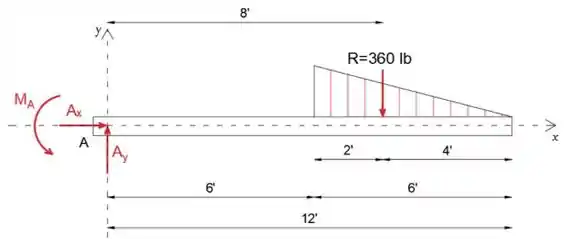
Passo 2
Ao igualar a soma das forças na direção x a zero, podemos determinar a força de reação Ax
igualando a soma dos momentos sobre o ponto A a zero, podemos determinar o par MA
Finalmente, ao igualar a soma das forças na direção y a zero, podemos determinar a força de reação Ay
Resposta
Exercícios de Livros Relacionados
Determine as coordenadas x e y do centroide da área sombreada.
O disco circular gira em relação a um eixo que passa por seu centro O e tem três furos de diâmetro d , posicionados como mostrado. Um quarto furo deve ser usinado no disco, no mesmo raio r , tal que o
Determine a profundidade h de um furo quadrado no cilindro circular sólido, para o qual a coordenada z do centro de massa terá o máximo valor possível..
Uma carga homogênea de propelente sólido para um foguete está na forma de um cilindro circular com um furo concêntrico de profundidade x . Para as dimensões mostradas, faça um gráfico de X - , a coord
Localize o centroide z - do solido.