Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 69
Determine a menor força horizontal exigida para começar a mover o bloco para a direita se a força da mola é de e o coeficiente de atrito estático em todas as superficies de contato em é . O cilindro em é liso. Despreze a massa de e .
Passo 1
O problema pede que descubra a menor força horizontal para mover bloco .
Bom galera, pra facilitar a gente começa fazendo um diagrama de corpo livre no bloco primeiro.
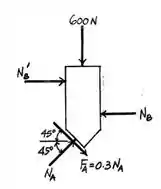
A força de atrito é:
Passo 2
A gente então precisa encontrar a força de reação , pra isso a gente analisa a vertical do bloco e fica assim:
E a gente encontra:
E assim a gente calcula o atrito:
Passo 3
Beleza, a gente já pode analisar as forças do calço com as forças que a gente já sabe, então vamos lá!
Comemando por mais um diagraminha de corpo livre:
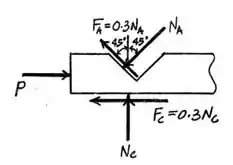
Vamos começar analisando a vertical porque a gente já tem e , e vamos ver o que a gente consegue:
Com isso a gente encontra:
E com isso:
Passo 4
Show de bola, agora com tudo que a gente já tem basta analisar a situação de equilibrio do calço na horizontal: