Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 72
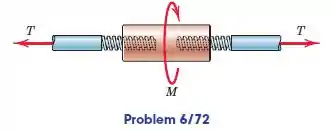
O colar rosqueado é usado para conectar dois eixos, ambos com fios à direita em suas extremidades. Os eixos estão sob uma tensão . Se os tópicos têm um diâmetro médio de e um avanço de , calcular o torque necessário para girar o colar em qualquer direção com os eixos impedidos de girar. O coeficiente de atrito é .
Passo 1
Oi pessoal? Vamos para mais um exercício?
O ângulo de fricção é dado por:
Substituindo o coeficiente de atrito, temos que:
Temos que:
Portanto:
Os dois ângulos agirão juntos em um eixo e um contra o outro no outro eixo. Portanto:
Resposta
Exercícios de Livros Relacionados
Se forças de binário F = 35N forem aplicadas ao punho da morsa, determine a força compressiva desenvolvida no bloco. Desconsidere o atrito no mancal A . A guia em B é lisa. O parafuso de rosca quadrad
Um esticador, semelhante ao mostrado na F i g u r a8.17 , é usado para tracionar o elemento ABda treliça. O coeficiente de atrito estático entre os parafusos com rosca quadrada e o esticador é μ s = 0
Se a força de retenção na placa A tiver de ser 2k N , determine o torque M que deverá ser aplicado ao parafuso para apertá-lo. O parafuso de rosca quadrada tem raio médio de 10m m e avanço de rosca de
Se a força de aperto necessária na placa A tiver de ser 50N , determine o torque M que deveráser aplicado ao punho do grampo “ C ” para apertá-lo contra a placa. O parafuso de rosca quadrada tem raio
O macaco consiste em um membro que possui um parafuso de rosca quadrada, com diâmetro médio de 12,5m m , avanço de rosca de 5m m e coeficiente de atrito estático u=0,4 . Determine o torque M que dever