Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 56

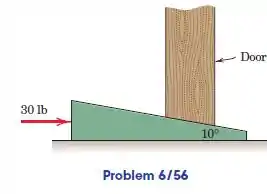
O batente da porta de 10 ° é inserido com uma horizontal para a direita força de 30   l b . Se o coeficiente de estática o atrito para todas as superfícies é μ s = 0,20 , determine os valores N U e N L das forças normais na parte superior e faces inferiores do batente da porta. Com o dado informações, você pode determinar a força P necessária extrair o batente da porta?

Passo 1

Oi pessoal? Vamos para mais um exercício?

Consideremos o deslocamento virtual S causado devido à força da mola:

S = θ - π 2

A energia armazenada na mola é dada pela seguinte equação:

W s = 1 2 k S 2

Substituindo os dados, temos que:

W s = 1 2 k ⋅ θ - π 2 2

O deslocamento virtual devido ao peso do bloco é dado por:

X = L 2 + L sen ⁡ θ

O trabalho realizado devido ao peso do bloco é dado por:

W b = W ⋅ X

Portanto:

W b = W L 2 + L sen ⁡ θ

A energia total do sistema será:

V = W s + W b

V = 1 2 k ⋅ θ - π 2 2 + W L 2 + L sen ⁡ θ

Passo 2

A condição de equilíbrio do sistema é a seguinte:

d V d θ = 0

Portanto:

d d θ 1 2 k ⋅ θ - π 2 2 + W L 2 + L sen ⁡ θ = 0

1 2 k ⋅ 2 θ - π 2 + W 0 + L cos ⁡ θ = 0

- W L cos ⁡ θ = k θ - π 2

Podemos fazer uma aproximação para a serie do cosseno que vale:

cos ⁡ θ = 1 - θ 2 2

Portanto:

W = k L 1 - θ 2 2 θ - π 2

Resposta

W = k L 1 - θ 2 2 θ - π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O dispositivo mostrado é usado para ajuste grosseiro da altura de um aparato experimental sem uma mudança em sua posição horizontal. Por causa da junta corrediça em A, girar o parafuso não gira a pern
Determine o torque M que deve ser aplicado à alça do parafuso para começar a mover o bloco de 100 lb para cima na inclinação de 15 ∘. O coeficiente de atrito estático entre o bloco e a inclinação é 0,
Repita Prob. 6/64, somente agora o bloco de concreto de 27 kg começa a se mover para baixo na inclinação de 20 ∘ conforme mostrado. Todas as outras condições permanecem como no Prob. 6/64.
O macaco mostrado foi projetado para levantar carros de carroceria pequena. O parafuso é rosqueado no colar articulado em B e o eixo gira em um rolamento de esferas em A. A rosca tem um diâmetro médio
Para ambas as condições (a) e (b), conforme declarado no Prob. 6/66, determine a magnitude e a direção da força P necessária para começar a abaixar o corpo de 100 lb.