Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 70
Determine a tensão de flexão máxima absoluta no pino de de diâmetro.
Passo 1
Primeiramente, vamos calcular :
Podemos então fazer o diagrama:
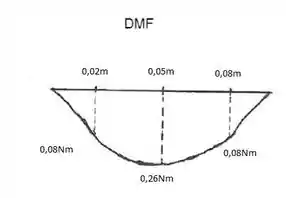
Passo 2
Claramente, o momento máximo é de 0,26Nm. Logo, a tensão máxima será:
Resposta
Exercícios de Livros Relacionados
Sabendo-se que uma viga de seção transversal, como mostrado, é encurvada em torno de um eixo horizontal e está submetida a um momento fletor de 5,7k N ⋅ m , determinar a intensidade total da força atu
A viga de seção transversal, como indicado, é extrudada de uma liga de alumínio com σe = 310 MPa e σu = 480 MPa. Usando um coeficiente de segurança 3,0, determinar o maior momento que pode ser aplicad
Sabendo-se que o momento mostrado atua no plano vertical e que cada raio interno é igual a 25mm, determinar a tensão nos pontos A e B.
Duas forças verticais são aplicadas a uma viga de seção transversal mostrada. Determinar as máximas tensões de tração e compressão na porção BC da viga.
Duas forças verticais são aplicadas a uma viga de seção transversal mostrada. Determinar as máximas tensões de tração e compressão na porção BC da viga.