Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 58
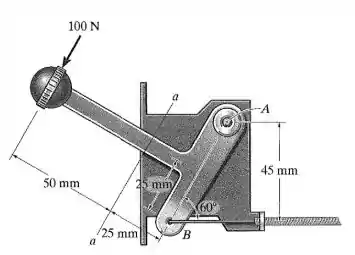
A alavanca de controle é usada em um cortador de grama de empurrar. Determine a tensão de flexão máxima na seção a-a da alavanca se uma força de for aplicada ao cabo. A alavanca é suportada por um pino em A e um cabo em B. A seção a-a é quadrada por .
Passo 1
Fala ai galerinha bonita, tudo jpoia?!
Para gente achar a tensão máxima, precisamos do momento máximo.
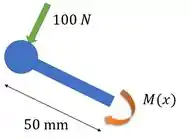
A gente quer o momento máximo na seção . Nessas questões de achar esforços internos, podemos partir nosso elemento na seção que foi pedida, e olhar só para o lado onde todas as forças já estão definidas.
No nosso caso, vamos partir nosso elemento em e olhar só para a esquerda. Aí nós colocamos a componente do momento nessa seção, para gente determinar pelas equações de equilíbrio o valor do momento na seção.
Vamos botar isso num DCL:
Passo 2
Com isso, podemos determinar a tensão máxima, pela fórmulinha:
Ela acontece na maior distância da linha neutra. Ou seja, em .
Calculando o momento de inércia da seção quadrada :
Aí só falta substituir tudo o que a gente tem na fórmulinha: