Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 99
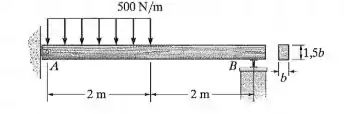
A viga de madeira tem seção transversal retangular na proporção mostrada na figura. Determine a dimensão b exigida se a tensão de flexão admissível for .
Passo 1
Falaa! Então, a ideia é dimensionar essa seção. Aí a gente precisa olha ela nas situações mais extremas. A tensão normal nesse caso só será causada pelo momento. Vamos começar achando o momento máximo nessa viga.
Primeiramente, vamos determinar as reações:
Passo 2
Com isso, a gente consegue fazer o diagrama de momento para essa viga. Considerando como positivo o sentido anti-horário.
- Para : :
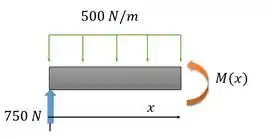
- Para : :
Aí desenhando o diagrama e achando o valor do momento máximo, temos:
Como podemos ver, o momento máximo vale .
Passo 3
A gente tem o mometo máximo e a tensão admissível. Queremos dimensionar a seção b. Podemos pensar na fórmulinha da tensão para o momento.
Se a tensão e o momento forem máximos:
As outras grandezas estão em função de . Então a gente consegue achar por essa expressão!
O momento de inércia da nossa seção será dado por:
E é o ponto da seção mais lnge do eixo do momento, ou seja, vale metade da altura da seção.
Passo 4
Substituindo tudo na equação do momento: