Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas de Revisão - Ex. 200

Determine a tensão máxima em cada um dos elementos de máquina mostrados.

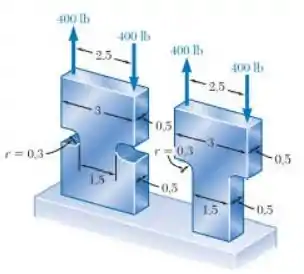
Passo 1

Fala aí, galera. Beleza? Bora resolver mais um exercício pra tirar aquele notão.

Este problema nos pede para determinarmos a tensão máxima em cada um dos elementos de máquina mostrados. Primeiro, devemos determinar o momento. Ele vai ser igual em todos os casos e vai ser dado por:

M = 400 2,5 M = 1000   l b ∙ i n

Em seguida, vamos calcular o momento de inércia para a seção mínima:

I = 1 12 0,5 1,5 3 = 0,140625   i n 4

E enão, podemos encontrar a distância para a linha neutra é, que é a metade do comprimento da seção mínima. Logo:

c = 0,75   i n

Assim:

D d = 3 1,5 = 2 r d = 0,3 1,5 = 0,2

Com isso, a tensão máxima vai ser:

σ m á x = K M c I

Onde K = 1,75 . Vale lembrar que o valor de K é tabelado. Logo:

σ m á x = 1,75 1000 0,75 0,140625 σ m á x = 9,33   k s i

Passo 2

E para o outro elemento de máquina, vamos repetir o processo para encontrarmos a tensão máxima. Temos:

D d = 3 1,5 = 2 r d = 0,3 1,5 = 0,2

Com isso, a tensão máxima vai ser:

σ m á x = K M c I

Onde K = 1 , 50 . Portanto:

σ m á x = 1 , 50 1000 0,75 0,140625 σ m á x = 8,0   k s i

É isso, galera!!! Bora zerar esse livro?

Resposta

σ m á x = 9,33   k s i

σ m á x = 8,0   k s i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.