Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 21
A força centrada é aplicada a um pilar curto conforme mostrado. Sabendo que as tensões no plano são e , determine (a) o ângulo que o plano forma com a horizontal, (b) a tensão de compressão no pilar.
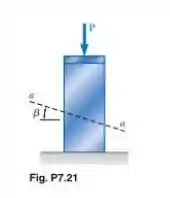
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora pra outra questão.
Neste caso, sabemos que:
Fazendo o ciclo de Mohr:
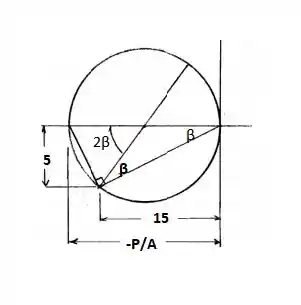
Logo:
Passo 2
Agora, basta achar a tensão. Ela será dada por:
Portanto, substituindo e isolando :
Resposta
Exercícios de Livros Relacionados
Determine o valor da carga P que provocará a tensãonormal máxima σ m á x á = 200 MPa na seção a-a do elo.
Se P = 15 kN, desenhe o gráfico da distribuição de tensão que age na seção transversal a-a do elo fora de centro.
A pressão do ar no cilindro será aumentada se forem exercidas as forças P = 2 kN nos dois pistões, cada qual com raio de 45 mm. Se a espessura da parede do cilindro for 2 mm. determine o estado de ten
O bloco está sujeito às três cargas axiais mostradas na figura. Determine a tensão normal desenvolvida nos pontos A e B. Despreze o peso do bloco.
O suporte de parede tem espessura de 6 mm e é usado para suportar as reações verticais da viga carregada, como mostra a figura. Se a carga for transferida uniformemente para cada alça do suporte, dete