Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 25

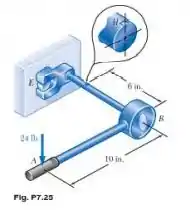
Um mecânico usa um pé de cabra para soltar um parafuso em E .   Sabendo que o mecânico aplica uma força vertical de 24   l b   em A ,   determine as tensões principais e a máxima tensão de cisalhamento no ponto H ,   localizado no topo do eixo de 3 4 i n   de diâmetro.

Passo 1

Fala aí, galerinha. Tudo bem com vocês? Partiu mais uma questão!

O primeiro passo para esta questão é determinar as tensões normal e de cisalhamento. Sabemos que a tensão de cisalhamento é:

τ = T c J

Onde T   é o momento torsor, c   é a distância da linha neutra e J   é o momento polar de inércia.

Portanto, teremos que:

J = π c 4 2 = 0,031   i n 4

τ = T c J = 240 × 0,375 0,031 = 2897   p s i = 2,897   k s i

Já a tensão normal, é dada por:

σ = - M y I

Onde M   é o momento fletor, y   é a distância da linha neutra e I   é o momento de inércia. Logo, substituindo:

I = 1 2 J = 0 , 015   i n 4

Portanto:

σ = 144 × 0,375 0,049 = 3477   p s i = 3,477   k s i

Passo 2

Agora, temos o seguinte:

σ x = 3,477     k s i

σ y = 0

τ x y = 2,897   k s i

Portanto, vamos usar esses dados para calcularmos o raio do círculo de Mohr:

R = σ x - σ y 2 2 + τ x y 2

Substituindo:

R = 3,378   k s i

Agora, vamos calcular as tensões máxima e mínima. Para isso, temos que achar o centro do círculo, ele será dado pela tensão média:

σ m é d = 1 2 σ x + σ y = 1,738   k s i

Ou seja, as tensões máxima e mínima serão:

σ m á x = σ m é d + R

σ m í n = σ m é d - R

Logo:

σ m á x = 5,12   k s i

σ m í n = - 1,640   k s i

Passo 3

Por fim, sabemos que a tensão máxima cisalhante será igual ao raio do nosso círculo e, portanto:

τ m á x = R = 3,378   k s i

Resposta

σ m á x = 5,12   k s i

σ m í n = - 1,640   k s i

τ m á x = R = 3,378   k s i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O parafuso da prensa exerce uma força de compressão de 2,5 kN nos blocos de madeira. Determine a tensão normal máxima desenvolvida ao longo da seção a-a. Nesse lugar, a seção transversal é retangular
O apoio está sujeito à carga de compressão P. Determine as tensões normais absolutas máximas e mínimas que agem no material.
A tampa do tanque cilíndrico é parafusada ao tanque ao longo das abas. O tanque tem diâmetro interno de 1,5 m e espessura da parede de 18 mm. Considerando que a maior tensão normal não deve ultrapassa
O apoio tem seção transversal circular, cujo raio aumenta linearmente com a profundidade. Se for submetido à carga de compressão P, determine as tensões normais máxima e mínima que agem no material.
O olhal está sujeito à força de 250 N. Determine as tensões de tração e compressão máxima na seção a-a. A seção transversal é circular e tem 6 mm de diâmetro. Use a fórmula da viga curva para calcular