Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 46
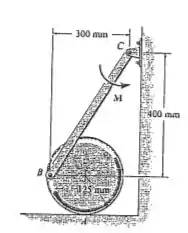
O disco de se apoia sobre a superfície para a qual o coeficiente de atrito estático Se , determine a força de atrito em .
Passo 1
Desejamos encontrar o valor da força de atrito no ponto . Para isso, tomemos o seguinte diagrama de forças
Tomemos, agora, as equações de equilíbrio para encontrarmos o que desejamos. Dessa forma, vamos analisar primeiramente para a barra
Já para o disco vamos ter
Resolvendo o sistema formado pelas equações acima vamos ter
O valor da força de atrito máxima é
Como esse valor é maior do que o que encontramos para , então, para nosso caso não há movimento do disco
Resposta
Exercícios de Livros Relacionados
O bloco A tem massa de 50k g e repousa sobre uma superfície para a qual μ s = 0,25 . Se o coeficiente de atrito estático entre a corda e o pino fixo em C é μ s ' = 0,3 , determine a maior massa do cil
O bloco A se apoia sobre a superfície para a qual μ s = 0,25 . Se a massa do cilindro suspenso D é 4k g , determine a menor massa do bloco A para que ele não deslize ou tombe. O coeficiente de atrito
Os blocos A e B têm massas de 20 kg e 10 kg, respectivamente. Usando os coeficientes de atrito estático indicados, determine a maior massa do bloco D sem causar movimento.
A roda está sujeita a um torque de M=50Nm . Se o coeficiente de atrito cinético entre a cinta de freio e a borda da roda é u k=0,3 , determine a menor força horizontal P que deverá ser aplicada à alav
Uma correia transportadora é usada para transferir material granular e a resistência ao atrito no topo da correia é F=500N . Determine o menor alongamento da mola presa ao eixo móvel da polia livre B