Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 59
O anel semicircular de massa e raio está soldado no eixo vertical, que permite que o anel gire no plano horizontal em torno do eixo -. Se um torque é aplicado ao anel por meio de seu eixo, determine a expressão para a aceleração angular resultante do anel e para a força que atua no plano horizontal sobre o anel em quando o anel inicia o movimento a partir do repouso.
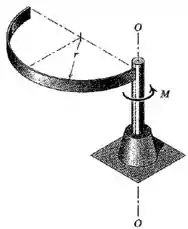
Passo 1
O momento de inércia de um anel completo de massa em relação a um eixo como o - da figura é:
Quando tomamos um anel semicircular, a forma da expressão para o momento de inércia não muda, apenas trocamos o valor da massa, que passa a ser . Então
E então a expressão para a aceleração angular quando um torque é aplicado no eixo pode ser escrita com a seguinte fórmula:
Passo 2
Agora que sabemos a aceleração angular, podemos calcular a aceleração do centro de massa do anel:
Onde é a distância entre o centro de massa e o eixo -. Então, pela segunda lei de Newton:
E a única força agindo na direção tangencial é justamente a força que atua sobre o anel, fazendo-o girar:
Passo 3
Falta encontrar uma expressão para :
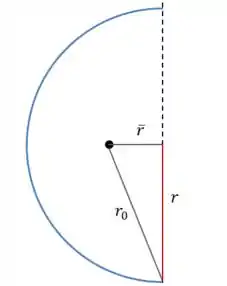
E a distância entre o centro de massa do anel semicircular e o centro do círculo pode ser consultada em uma tabela:
E então:
Resposta
A aceleração angular é , e a força é .