Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 121
O dispositivo mostrado é usado para ajuste grosseiro de altura de um aparato experimental sem mudança da sua posição horizontal. Devido à junta deslizante em , o giro do parafuso não causa giro no suporte cilíndrico acima de . O diâmetro médio da rosca é 12 mm e o coeficiente de atrito vale 0,15. Em um projeto conservador que despreza o atrito na junta deslizante, qual seria o menor número de roscas por centímetro para garantir que o parafuso de rosca simples não gire por si só sob o peso do aparato?
Passo 1
A condição para o não deslizamento de um parafuso com rosca quadrada é dada por:
Sendo a angulação da rosca e o ângulo de atrito entre a rosca do eixo e a rosca do parafuso. O caso limite o corre quando . Através dessa fórmula, iremos encontrar a inclinação da rosca em relação à horizontal e o número de nesse caso.
Passo 2
O ângulo é calculado através do coeficiente de atrito. A relação é:
Como , encontramos o ângulo:
Então:
Passo 3
O ângulo pode ser mostrado abrindo uma volta completa da rosca em um plano. Teremos um triângulo retângulo com largura igual à circunferência do parafuso e altura igual ao passo da rosca:
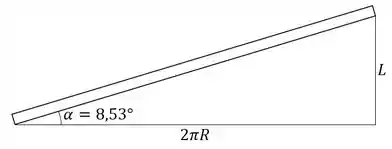
O raio do parafuso é de . Então calculamos seu passo:
O passo é o número de centímetros por rosca. Como queremos o número de roscas por centímetro, basta calcularmos o inverso: