Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 124
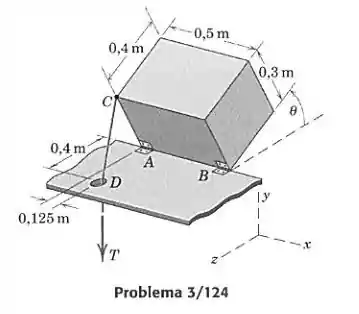
O sistema do Prob. 3/107 é mostrado novamente aqui. Só que agora, o sólido homogêneo de 125 kg está mostrado girado por um ângulo em torno do eixo da dobradiça. Determine e plote as seguintes quantidades como funções de , na faixa : , , , , e . A dobradiça em não pode exercer esforço axial. Assuma que todas as componentes das forças na dobradiça estão nas direções coordenadas positivas.
Passo 1
Vamos representar as forças atuantes no sólido em um diagrama de corpo livre. A força em não tem componente , como especificou o enunciado:
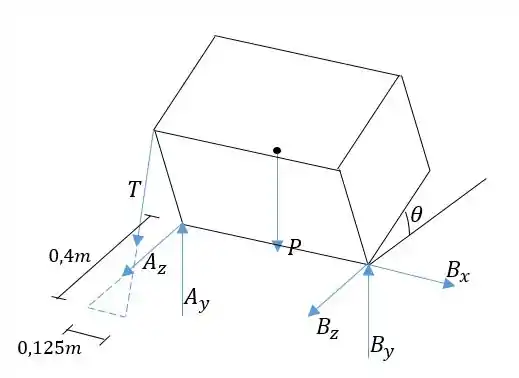
Passo 2
Temos 6 incógnitas, então precisamos de 6 equações de equilíbrio: Soma das forças em cada uma das 3 direções e soma dos momentos em torno de cada um dos eixos. Primeiro vamos determinar a expressão de em termo de seu módulo. Temos:
Onde é o vetor unitário que determina a direção de . Vamos calcular . Olhando o perpendicularmente a , vemos assim:
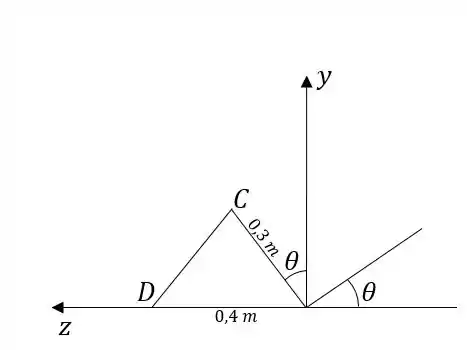
Se considerarmos a origem em , as coordenadas de e são:
Então:
Vamos agora calcular o módulo:
Então:
Passo 3
Agora já sabemos as componentes de em função do módulo, vamos às equações. O peso é igual a . Vamos começar pelas forças:
Agora os momentos em torno dos eixos. Vamos considerar a origem em , pois passa nesse ponto e não participa das contas. As coordenadas de o centro de massa em relação a são:
Vamos então às 3 equações:
Passo 4
Através do auxílio de um computador, resolvemos as equações e chegamos às soluções:
Passo 5
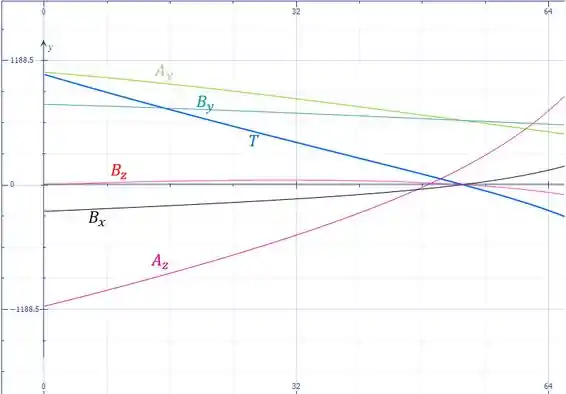
Representamos as forças em um gráfico:
