Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 108
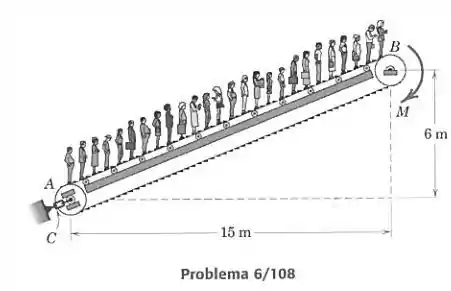
A correia sem fim de uma escada rolante passa em volta do tambor esticador e é movimentada por um torque aplicado ao tambor . A força trativa na correia é ajustada por um esticador em , que produz uma força trativa inicial de 4,5 kN em cada lado da correia, quando a escada está sem carga. Para o projeto desse sistema, calcule o coeficiente de atrito mínimo entre o tambor e a correia para impedir o deslizamento se a escada transporta 30 pessoas, com 70 kg em média cada uma, uniformemente distribuídas ao longo da correia. (Nota: Pode-se mostrar que o aumento da força trativa na correia no lado superior do tamnor e a redução da força trativa na correia no tambor inferior são, cada, iguais à metade da componente do peso combinado dos passageiros ao longo da escada.)
Passo 1
Como não há deslizamento entre a correia e o tambor, é válida a fórmula para o equilíbrio de uma corda enrolada em torno de uma superfície, dada a seguir:
Sendo e as trações maior e menor nas extremidades da corda e o ângulo total de enrolamento no tambor, no caso igual a , o ângulo de meia volta. Em cima, temos a tração de 4,5 kN mais metade da tração adicional causada pelo peso das pessoas. Em baixo, temos a tração de 4,5 kN menos metade da tração adicional causada pelo peso das pessoas.
Passo 2
Primeiro vamos definir os valores das trações e . Temos 30 pessoas, então o peso total combinado é:
O ângulo de inclinação da escada é:
Então a componente do peso paralelo à escada é:
Assim, achamos e , subtraindo e somando metade desse valor a 4,5 kN:
Passo 3
Agora aplicaremos a fórmula: