Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 7
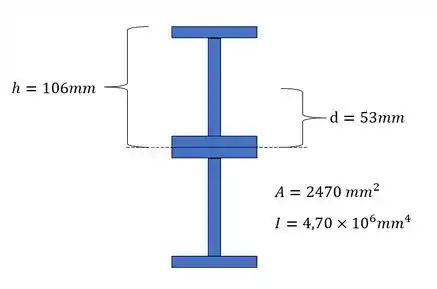
Duas barras de perfil de aço laminado , são soldadas conforme mostra a figura. Sabendo que para a liga de aço usada e , e usando um coeficiente de segurança de , determine o maior momento que pode ser aplicado quando o conjunto é flexionado em relação ao eixo .
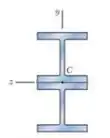
Passo 1
Fala galerinha, nosso objetivo com essa questão é determinar o momento máximo que podemos aplicar na nossa estrutura, para isso temos que saber a máxima tensão que age nela.
Então temos que lembrar que a nossa fórmula de tensão quando temos um momento agindo é dada por:
E cada terminho desse é bem tranquilo de determinar, beleza? Então vamos lá.
Passo 2
Existem dois termos que não dependem em nada dos pontos aplicado, então vamos determinar eles primeiro.
- (tensão admissível, ou tensão máxima)
- I (momento de inércia)
Essa o enunciado da de graça pra gente, assim temos que:
E como queremos saber o momento máximo que age na seção quando temos um fatore de segurança de 3, devemos fazer a seguinte conta:
E sabemos que:
Assim teremos que:
O momento de inércia pode parecer muito complexo, mas é muito de boas, para isso precisamos dos dados da nossa seção, assim podemos obter no próprio livro os seguintes dados:
E como as nossas seções são iguais, podemos definir a fórmula como:
E cada um desses itens é dado por:
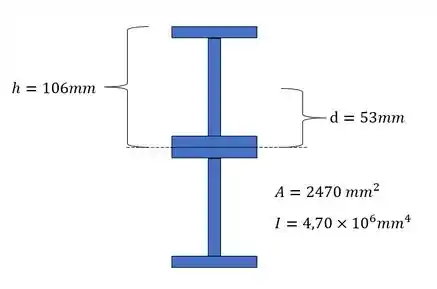
Agora só precisamos do y e para termos o momento máximo, precisamos de um ponto especifico.
Passo 3
Para termos o momento máximo, precisamos do y mais distante da LN, porque assim teríamos a tensão máxima que age na nossa seção, e por consequência, teremos o momento máximo, dessa forma, teremos que:
