Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 82

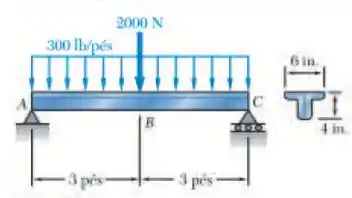
Duas cantoneiras L4 x 3 laminadas são parafusadas por uma das abas e utilizadas para suportar o carregamento mostrado. Sabendo que a tensão normal admissível para o aço utilizado é de 24 ksi, determine a menor espessura e cantoneira que poderá ser utilizada.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine a menor espessura e cantoneira que poderá ser utilizada. Desenhando o diagrama de corpo livre temos :D

Passo 2

Então galera por simetria, A = C , vamos fazer o somatório das forças em Y temos:

+ ↑ ∑ F y = 0 :           A + C - 200 - 6   x   300   = 0 A = C = 1900   l b

Agora devemos calcular os esforços cortantes vem comigo!!

V A = 1900   l b = 1,9   k i p s V B - = 1900 - 3   x   300 = 1000   l b = 1   k i p V B + = 1000 - 2000 = - 1000   l b = - 1   k i p V C = - 1000 - 3   x   300 = - 1900   l b | = - 1,9   k i p

Agora sim podemos desenhar o diagrama:

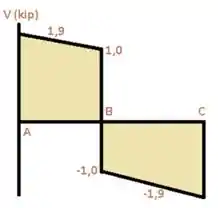
Passo 3

Calculando as Áreas temos:

A para B: 1 2   x   3   x   1,9 + 1 = 4,35   k i p * f t

B para C: 1 2   x   3   x   - 1 - 1,9 = - 4,35   k i p * f t

Passo 4

Agora sim gurizada partiu determinar os momentos :D

Momento de flexão: M A = 0

M B = 0 + 4,35 = 4,35   k i p * f t M C = 4,35 - 4,35 = 0

Máximo: M = 4,35   k i p * f t = 52,2   k i p * i n

Passo 5

Considerando a σ a l l = 24   k s i temos então:

Para seção que consiste em dois ângulos, S m i n = M σ a l l = 52,2 24 = 2,175   i n 3

Para cada ângulo, .

  S m i n = 1 2   x   2,175 = 1,0875   i n ³

Resposta

menor espessura permitida: t = 3 8 i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

sabendo que a tensão admissível para a viga mostrada é de 90M p a , determine o momento fletor M admissível quando o raio r dos adoçamentos é:8mm12mm
Ranhuras semicirculares de raio r devem ser fresadas nos lados de uma barra de aço, conforme mostra a figura. Usando uma tensão admissível de 8 k s i , determine o maior momento fletor que pode ser ap
Ranhuras semicirculares de raio r devem ser fresadas nos lados de uma barra de aço, conforme mostra a figura. Sabendo que M = 4k i p ∙ i n , determine a tensão máxima na barra quando o raio r das ranh
Um momento fletor M = 2k N m deve ser aplicado à extremidade de uma barra de aço. Determine a tensão máxima na barra:Considerando que a barra foi projetada com ranhuras semicirculares de raio r = 10 m
A tensão admissível usada no projeto de uma barra de aço é de 80M P a . Determine o maior momento fletor M que pode ser aplicado à barra.Considerando que a barra foi projetada com ranhuras semicircula