Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 65
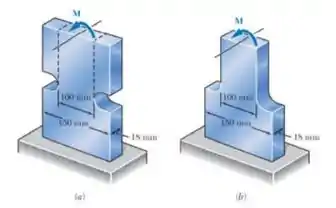
Um momento fletor deve ser aplicado à extremidade de uma barra de aço. Determine a tensão máxima na barra:
- Considerando que a barra foi projetada com ranhuras semicirculares de raio , como mostra a ,e.
- Se a barra for reprojetada com a remoção do material à esquerda e a direita das linhas tracejadas, como mostra a .
Passo 1
Nesse caso queremos determinar a máxima tensão que age na nossa estrutura, porém, precisamos notar que aqui estamos falando da um caso de concentração de tensões, e para casos de concentração de tensões, temos fórmulas especificas, dadas por:
E cada terminho desse é bem tranquilo de determinar, beleza? Então vamos lá, começar resolvendo tudo referido ao item A).
Passo 2
Vamos então ir determinando cada termo antes de usarmos na nossa equação, assim, temos que:
- Momento fletor
- I (momento de inércia)
- Y
- M (momento fletor)
- I (momento de inércia)
- Y
Esse é bem tranquilo, já que o enunciado já nos dá a tensão, assim, temos que:
Temos aqui duas seções, certo? Qual das duas usar? Pensa no seguinte, o momento vai ser o mesmo na seção maior e na seção menor, certo? Se ele fosse uma força(presta atenção, no caso ele não é, mas vamos supor que seja) se ele fosse uma força, onde surgiria a maior tensão? Na menor área ou na maior área? Pegou o esquema? Se queremos a MÁXIMA TENSÃO, temos que usar A MENOR SEÇÃO.
Como ela é retangular, basta usarmos a seguinte fórmula:
O valor de é a espessura da nossa seção, e essa é comum ao item a) e b), assim teremos que:
Esse você nem vai acreditar, usamos a menor seção para a inércia, certo? Ou seja, se estamos na menor seção, o y é a metade da altura da menor seção.
E veja só, agora só precisamos do valor de , certo? Como o calculo dele é um pouquinho diferente, vamos determinar ele no próximo passo.
Passo 3
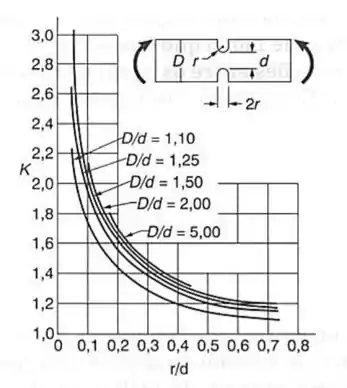
Para determinarmos o valor de , precisamos de um diagrama que nos dá o coeficiente de concentração de tensões, e para esse tipo de seção, esse diagrama é dado por:
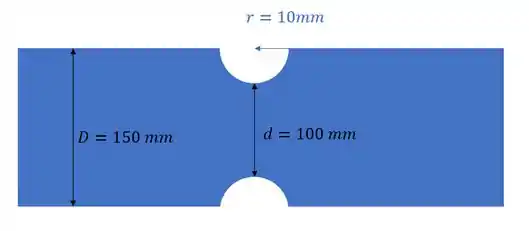
E sabemos que a nossa seção é dada por:
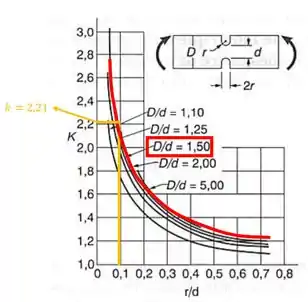
E assim olhando o nosso diagrama, teremos o seguinte .
Passo 4
Agora que temos tudo, podemos calcular as tensões máximas em cada um dos nossos itens, assim, teremos que:
Agora vamos calcular o item B).
Passo 5
E vamos usar a mesma fórmula do item A) mas com algumas diferenças.
E cada terminho desse é bem tranquilo de determinar, beleza? Então vamos lá.
Vamos então ir determinando cada termo antes de usarmos na nossa equação, assim, temos que:
Esse é bem tranquilo, já que o enunciado já nos dá o momento, assim, temos que:
Temos aqui duas seções, certo? Qual das duas usar? Pensa no seguinte, o momento vai ser o mesmo na seção maior e na seção menor, certo? Se ele fosse uma força(presta atenção, no caso ele não é, mas vamos supor que seja) se ele fosse uma força, onde surgiria a maior tensão? Na menor área ou na maior área? Pegou o esquema? Se queremos a MÁXIMA TENSÃO, temos que usar A MENOR SEÇÃO.
Como ela é retangular, basta usarmos a seguinte fórmula:
Como a menor seção é a espessura tem de base por de altura, teremos que:
Esse você nem vai acreditar, usamos a menor seção para a inércia, certo? Ou seja, se estamos na menor seção, o y é a metade da altura da menor seção, como a menor seção tem de altura, teremos que:
E veja só, agora só precisamos do valor de , certo? Como o calculo dele é um pouquinho diferente, vamos determinar ele no próximo passo.
Passo 3
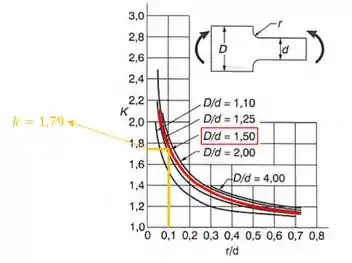
Para determinarmos o valor de , precisamos de um diagrama que nos dá o coeficiente de concentração de tensões, e para esse tipo de seção, esse diagrama é dado por:
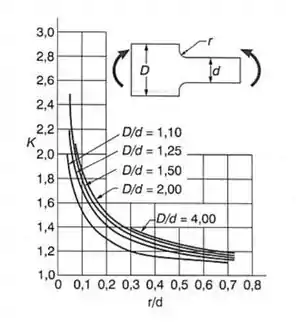
E sabemos que a nossa seção é dada por:
E veja que podemos determinar a nossa curva pela seguinte relação:
E precisamos da relação para o eixo horizontal dado por
E assim olhando o nosso diagrama, teremos o seguinte .
Passo 4
Agora que temos tudo, podemos calcular as tensões máximas em cada um dos nossos itens, assim, teremos que: