Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas de Revisão - Ex. 161

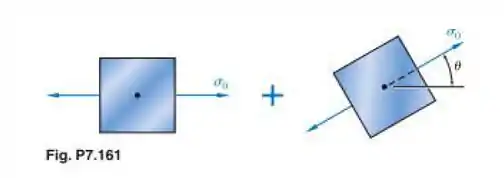
Determine os planos principais e as tensões principais para o estado plano de tensões que resulta da superposição dos dois estados planos mostrados.

Passo 1

Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos precisar encontrar as tensões nas direções x e y para o elemento que está rotacionado de um ângulo θ . Faremos isso utilizando as seguintes equações para a rotação:

σ x ' = σ x + σ y 2 + σ x - σ y 2 cos ⁡ 2 θ - τ x y s e n   2 θ

σ y ' = σ x + σ y 2 - σ x - σ y 2 cos ⁡ 2 θ - τ x y s e n   2 θ

τ x ' y ' = σ x - σ y 2 s e n   2 θ + τ x y cos ⁡ 2 θ

Fazendo isso podemos somar as tensões obtidas com aquelas para o primeiro elemento obtendo o estado resultante. Aí ficou fácil, basta substituir as expressões nas equações para as direções e tensões principais. Então vamos lá!

Passo 2

Beleza! Vamos começar escrevendo as tensões para o elemento rotacionado em função dos eixos x e y através das equações do passo 1. Sabendo que nesse elemento temos as seguintes tensões:

σ x ' = σ 0 ;                 σ y ' = 0 ;                     τ x ' y ' = 0

Então, as equações de transformação se tornam:

σ x = σ x ' + σ y ' 2 + σ x ' - σ y ' 2 cos ⁡ 2 θ - τ x ' y ' s e n   2 θ = σ 0 + 0 2 + σ 0 - 0 2 cos ⁡ 2 θ - 0

σ x = σ 0 2 + σ 0 2 cos ⁡ 2 θ

σ y = σ x ' + σ y ' 2 - σ x ' - σ y ' 2 cos ⁡ 2 θ - τ x ' y ' s e n   2 θ = σ 0 + 0 2 - σ 0 - 0 2 cos ⁡ 2 θ - 0

σ y = σ 0 2 - σ 0 2 cos ⁡ 2 θ

τ x y = σ x ' - σ y ' 2 s e n   2 θ + τ x ' y ' cos ⁡ 2 θ = - σ 0 - 0 2 s e n   2 θ + 0

τ x y = σ 0 2 s e n   2 θ

Beleza! Agora podemos somar essas expressões ao estado de tensão do elemento não rotacionado, que só possui σ x = σ 0 , então chegaremos no seguinte estado resultante:

σ x = σ 0 + σ 0 2 + σ 0 2 cos ⁡ 2 θ → σ x = 3 σ 0 2 + σ 0 2 cos ⁡ 2 θ

σ y = σ 0 2 - σ 0 2 cos ⁡ 2 θ

τ x y = σ 0 2 s e n   2 θ

Passo 3

Agora que encontramos as expressões para a tensão no sistema resultante, sabemos que a direção principal é dada por:

t g   2 θ P = 2 τ x y σ x - σ y

Substituindo as expressões encontradas no passo 2, teremos:

t g   2 θ P = 2 σ 0 2 s e n   2 θ 3 σ 0 2 + σ 0 2 cos ⁡ 2 θ - σ 0 2 - σ 0 2 cos ⁡ 2 θ = σ 0 s e n   2 θ σ 0 + σ 0 cos ⁡ 2 θ

Dividindo a expressão em cima e embaixo por σ 0 , teremos:

t g   2 θ P = s e n   2 θ 1 + cos ⁡ 2 θ

Agora vamos abrir as expressões para as somas de arco, então teremos:

t g   2 θ P = s e n θ cos ⁡ θ + s e n θ cos ⁡ θ 1 + cos ⁡ θ cos ⁡ θ - s e n θ   s e n   θ = 2 s e n θ cos ⁡ θ 1 + cos 2 ⁡ θ - s e n 2 θ

Da relação trigonométrica fundamental, temos:

s e n 2 θ + cos 2 ⁡ θ = 1 → s e n 2 θ = 1 - cos 2 ⁡ θ

Substituindo essa expressão na equação de cima, teremos:

t g   2 θ P = 2 s e n θ cos ⁡ θ 1 + cos 2 ⁡ θ - 1 - cos 2 ⁡ θ = 2   s e n θ cos ⁡ θ 2 cos 2 ⁡ θ → t g   2 θ P = s e n   θ cos ⁡ θ

Então, teremos:

t g   2 θ P = t g   θ → 2 θ P = θ → θ P = θ 2

Como sabemos que a outra direção principal fica do outro lado do círculo, ou seja, a 180° ou π radianos de distância, então teremos:

θ P = θ 2 + π

Essas são as duas direções principais para o nosso sistema. Agora bora encontrar as tensões principais.

Passo 4

Sabemos que as tensões principais serão dadas por:

σ a = σ m e d + R

σ b = σ m e d - R

Então precisamos encontrar expressões para a tensão média e para o raio do círculo de Mohr. Começando pela tensão média, teremos:

σ m e d = σ x + σ y 2

Substituindo as expressões conhecidas encontradas lá no passo 2, chegaremos em:

σ m e d = 3 σ 0 2 + σ 0 2 cos ⁡ 2 θ + σ 0 2 - σ 0 2 cos ⁡ 2 θ 2 → σ m e d = σ 0

Beleza! Agora vamos partir para o raio do círculo de Mohr, sabemos que sua equação é dada por:

R = σ x - σ y 2 2 + τ x y 2

Substituindo as expressões conhecidas, teremos:

R = 3 σ 0 2 + σ 0 2 cos ⁡ 2 θ - σ 0 2 - σ 0 2 cos ⁡ 2 θ 2 2 + σ 0 2 s e n   2 θ 2

R = σ 0 2 + σ 0 2 cos ⁡ 2 θ 2 + σ 0 2 s e n   2 θ 2

Passo 5

Agora vamos desenvolver a expressão encontrada para o raio:

R = σ 0 2 4 + σ 0 2 2 cos ⁡ 2 θ + σ 0 2 4 cos 2 ⁡ 2 θ + σ 0 2 4 s e n 2   2 θ = σ 0 2 4 1 + 2 cos ⁡ 2 θ + cos 2 ⁡ 2 θ + s e n 2   2 θ

Lembrando da relação fundamental trigonométrica que usamos no passo 3, temos que cos 2 ⁡ 2 θ + s e n 2   2 θ = 1 . Vamos abrir também a soma de arco de cos ⁡ 2 θ . Fazendo isso, a equação acima se torna:

R = σ 0 2 1 + 2 cos 2 ⁡ θ - s e n 2 θ + 1

Simmm! Vamos usar novamente a relação fundamental, com s e n 2 θ = 1 - cos 2 ⁡ θ , fazendo isso, a equação acima se torna:

R = σ 0 2 1 + 2 cos 2 ⁡ θ - 1 + cos 2 ⁡ θ + 1 → R = σ 0 2 4 cos 2 ⁡ θ → R = σ 0 cos ⁡ θ

Ufaaa! Demorou, mas conseguimos chegar no valor do raio. Agora basta substituir os valores conhecidos nas equações para as tensões principais, onde teremos:

σ a = σ m e d + R = σ 0 + σ 0 cos ⁡ θ → σ a = σ 0 1 + cos ⁡ θ

σ b = σ m e d - R = σ 0 - σ 0 cos ⁡ θ → σ b = σ 0 1 - cos ⁡ θ

Prooonto! Chegamos nas tensões principais que foram pedidas. Valeu pela companhia de novo!!

Resposta

θ P = θ 2 ;   θ P = θ 2 + π

σ a = σ 0 1 + cos ⁡ θ ;   σ b = σ 0 1 - cos ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O círculo de Mohr mostrado corresponde ao estado de tensão dado nas Figs. 7.5a e b. Notando que σ x ' = OC + (CX’) cos ⁡ 2 θ p - 2 θ e que τ x ' y ' = C X ' s e n 2 θ p - 2 θ , determine as expressões
Resolva o Problema 7.81 usando o critério da tensão de cisalhamento máxima.
O estado plano de tensão indicado ocorre em um componente de máquina feito de um aço com σ E = 45k s i . Usando o critério da energia de distorção máxima, determine se ocorre o escoamento quando (a) τ
O estado plano de tensão indicado ocorre em um componente de máquina feito de um aço com σ E = 325M P a . Usando o critério da energia de distorção máxima, determine se ocorre o escoamento quando (a)
Para o estado de tensão do Problema 7.69, determine (a) o valor de σ y para o qual a tensão de cisalhamento máxima seja a menor possível e (b) o valor correspondente da tensão de cisalhamento.