Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 78
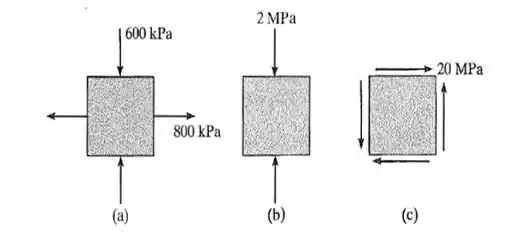
78. Obtenha o círculo de Mohr que descreve cada um dos seguintes estados de tensão.
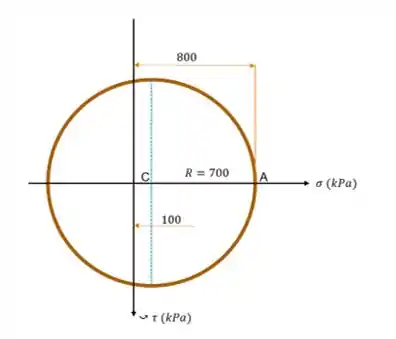
Passo 1
(a) Da figura do enunciado, tiramos que:
A primeira coisa que temos que fazer é determinar a tensão média , que será o centro do nosso primeiro círculo, através da fórmula abaixo:
E substituindo os valores numéricos correspondentes, chegamos à:
Depois, o próximo passo é achar o raio através da tensão máxima de cisalhamento , que é dada por:
Trocando os valores de cada variável, obtemos nossa tensão máxima como:
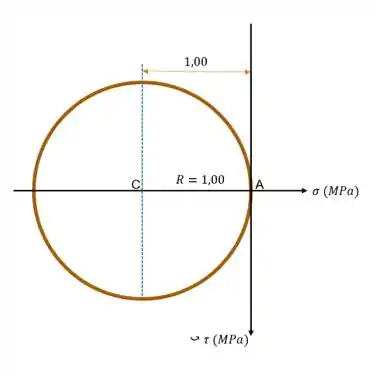
Passo 2
(b) Da figura do enunciado, tiramos que:
A primeira coisa que temos que fazer é determinar a tensão média , que será o centro do nosso segundo círculo, através da fórmula abaixo:
E substituindo os valores numéricos correspondentes, chegamos à:
Depois, o próximo passo é achar o raio através da tensão máxima de cisalhamento , que é dada por:
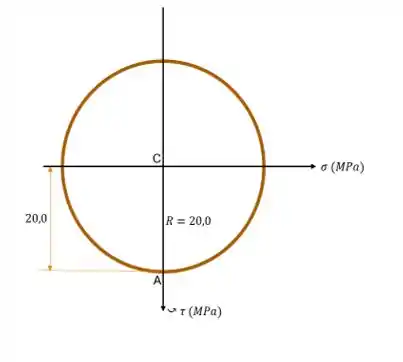
Passo 3
(c) Da figura do enunciado, tiramos que:
A primeira coisa que temos que fazer é determinar a tensão média , que será o centro do nosso terceiro círculo, através da fórmula abaixo:
E substituindo os valores numéricos correspondentes, chegamos à:
Depois, o próximo passo é achar o raio através da tensão máxima de cisalhamento , que é dada por:
E o nosso círculo vai ter então, a seguinte cara:
Resposta
Ei, a resposta está no passo a passo :)