Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 33
Considere a orientação geral dos três extensômetros em um único ponto como mostra a figura. Escreva um código computacional que possa ser usado para determinar as deformações principais no plano e a deformação por cisalhamento máxima no plano em um ponto. Mostre uma aplicação do código usando os valores
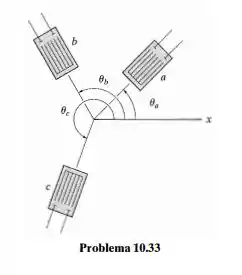
Passo 1
% CÓDIGO MATLAB
% A melhor forma de resolver essa questão é através de um sistema
% linear de equações.
clear
clc
% ====== Entrada de dados ======
ea = 160e-6;
eb = 100e-6;
ec = 80e-6;
tht_a = 40; % graus
tht_b = 125; % graus
tht_c = 220; % graus
% Descomente para testar com os dados do exemplo 10.8
% ea = 60e-6;
% eb = 135e-6;
% ec = 264e-6;
% tht_a = 0; % graus
% tht_b = 60; % graus
% tht_c = 120; % graus
% ====== Conversão de unidades ======
tht_a = tht_a*pi/180; % rad
tht_b = tht_b*pi/180; % rad
tht_c = tht_c*pi/180; % rad
% ====== Gerando matrizes pro sistema linear ======
y = [ea;
eb;
ec];
A = [(cos(tht_a))^2, (sin(tht_a))^2, cos(tht_a)*sin(tht_a);
(cos(tht_b))^2, (sin(tht_b))^2, cos(tht_b)*sin(tht_b);
(cos(tht_c))^2, (sin(tht_c))^2, cos(tht_c)*sin(tht_c)];
% E x será composto por:
% x = [ex;
% ey;
% ez];
x = inv(A)*y
Passo 2
Se utilizarmos os dados fornecidos pela questão o resultado será:
Estes valores são claramente absurdos!
Mas isso ocorre por um motivo. Observe os ângulos fornecidos pela questão:
Percebeu?! Os ângulos e estão defasados entre si em 180º. Isso resulta que seus cossenos e senos terão sinais opostos! Mas a equação 10.16 que usamos para calcular as rosetas eleva esses valores ao quadrado. O resultado final é que o nosso sistema possui duas equações iguais!
Isso fica óbvio quando pedimos o valor da matriz A
A primeira e última linha da matriz são iguais. E por isso o nosso, com os dados fornecidos pela questão, o sistema é Linearmente Dependente e NÃO possui solução única.
Passo 3
Vamos fazer uma análise sobre a prática da engenharia:
Se os dados que a questão forneceu tivessem sidos medidos por um engenheiro ou técnico, esta pessoa teria feito uma medida inapropriada, e seria necessário ter novas medidas feitas corretamente.
Resposta
Ei, a resposta está no passo a passo :)