Os elementos de um tubo de desodorante em barra são mostrados na figura. Para subir a barra do desodorante , o disco é girado. O eixo rosqueado se conecta as roscas da base móvel ; o eixo não tem roscas no suporte fixo . A rosca quadrada dupla de 6 mm de diâmetro tem o passo de 5 mm. Determine o coeficiente de atrito estárico para o qual o desodorante não descerá sob ação da força . Despreze o atrito em .
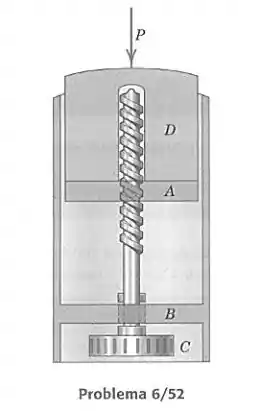
Passo 1
A força que a rosca da base móvel realiza na rosca quadrada é composta por uma força normal e uma força de atrito paralela à superfície de contato. Vamos representar essas forças atuando numa pequena parte da rosca quadrada:
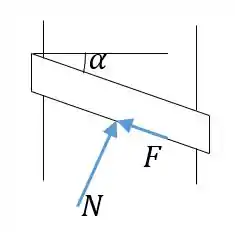
Para que a rosca não gire, não pode haver momento em torno de seu eixo, então a resultante de e deve ser vertical. Sabe-se que o ângulo entre a resultante e a linha normal à superfície deve ser , sendo que:
Vamos então representar nossa resultante :
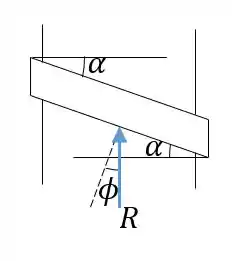
Pela figura conseguimos concluir que:
Passo 2
Vamos então encontrar pela relação entre e . O ângulo entre a rosca e a horizontal pode ser obtido abrindo uma volta completa da rosca, sabendo que seu passo é de 5 mm e o raio de 3 mm:
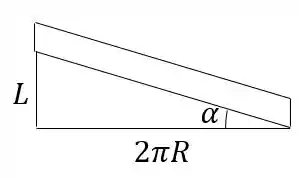
Então
Encontramos então :