Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 89

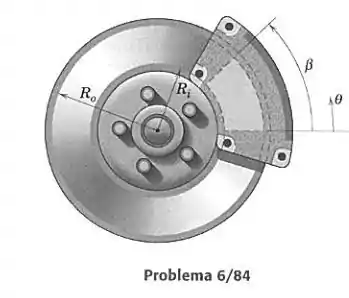
Um disco de freio de automóvel consiste em um rotor de faces planas e uma pinça que tem uma sapata em cada lado do rotor. Para forças P idênticas atuando atrás de cada sapata, mostre que o momento aplicado ao cubo da roda é independente da faixa angular β das sapatas. A variação da pressão com θ mudaria o momento?

Passo 1

Temos aplicado por cada sapata uma força total P , que é aplicada à área de contato entre a sapata e a face circular com uma pressão constante p . Queremos calcular o momento total realizado por cada pequena força de atrito d F em torno do eixo central. Vamos representar a forças atuantes em uma pequena área d A da face circular, que mostramos inclinada:

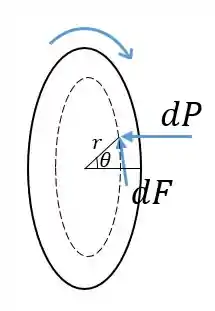
Como sabemos que a força de atrito é igual à normal vezes o coeficiente de atrito, cada força d F é igual a:

d F = μ   d P = μ p   d A

Calculando o momento causado em uma área pequena d A e integrando para o raio variando entre R i e R o   e o ângulo entre e β , vamos encontrar o momento total. Não podemos esquecer de multiplicar o resolutado final por 2, já que são duas sapatas aplicando momento.

Passo 2

Tendo a força d F de atrito causada a uma pequena área d A , situada a r m do centro e com angulação θ , calculamos o pequeno momento d F causado por essa força no centro:

d M = r   d F = μ p r   d A

Mas a área d A pode ser dada por:

d A = d r ⋅ d l = d r ⋅ r d θ = r d r   d θ

Então:

d M = μ p r   d A = μ p r   d r   r d θ = μ p r 2 d r   d θ

Passo 3

Agora devemos calcular a integral dupla:

M = ∫ 0 β d θ ∫ R i R o μ p r 2 d r  

Só temos na esquerda d θ então achamos diretamente ∫ 0 β d θ = β :

M = μ p β ∫ R i R o r 2 d r = μ p β r 3 3 R i R o = μ p β ( R i 3 - R o 3 ) 3

Como a pressãp p é constante, e sabemos que a força total P é dada pela pressão vezes a área:

P = p A = p ⋅ β 2 π π R o 2 - π R i 2 = p β R i 2 - R o 2 2

⇒ p = 2 P β R i 2 - R o 2

⇒ M = μ β ( R i 3 - R o 3 ) 3 ⋅ 2 P β R i 2 - R o 2 = 2 μ P 3 R i 3 - R o 3 R i 2 - R o 2

Então o momento total é:

2 M = 4 μ P 3 R i 3 - R o 3 R i 2 - R o 2

Que de fato não depende de β .

Passo 4

Se tivéssemos uma pressão p , variável com θ , nossa integral para o momento então ficaria:

M = ∫ 0 β p d θ ∫ R i R o μ r 2 d r = μ ( R i 3 - R o 3 ) 3 ∫ 0 β p d θ

E nossa força P seria na verdade calculada da seguinte maneira:

P = ∫ p   d A = ∫ 0 β p d θ ∫ R i R o r d r = R i 2 - R o 2 2 ∫ 0 β p d θ

Então:

∫ 0 β p d θ = 2 P R i 2 - R o 2 ⇒ M = μ ( R i 3 - R o 3 ) 3 ⋅ 2 P R i 2 - R o 2 = 2 μ P 3 R i 3 - R o 3 R i 2 - R o 2

Que é o mesmo resultado de antes.

Resposta

2 M = 4 μ P 3 R i 3 - R o 3 R i 2 - R o 2

Não depende de β , nem do tipo da função p ( θ ) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força P necessária para superar a resistência ao rolamento e suportar o cilindro de 50k g se ele rolar para baixo no plano inclinado com velocidade constante. O coeficiente de resistência
A barra em L se ajusta livremente em um pino de 12m m de diâmetro. Determine a força P necessária que seja apenas suficiente para girar a barra em sentido horário. O coeficiente de atrito estático ent
Determine a menor força horizontal P que precisa ser exercida sobre o bloco de 100k g para movê-lo para frente. Os roletes pesam 250N ( ≈ 25k g ) cada, e o coeficiente de resistência ao rolamento nas
A barra em L se ajusta livremente em um pino de 12m m de diâmetro. Se P = 205N , a barra está então rpestes a girar em sentido anti-horário. Determine o coeficiente de atrito estático entre o pino e a
Determine a força P necessária para superar a resistência ao rolamento e puxar o cilindro de 50k g no plano inclinado com velocidade constante. O coeficiente de resistência ao rolamento é a = 15m m .