Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 177
Represente a resultante das três forças e do binário por um sistema força-binário localizado no ponto .
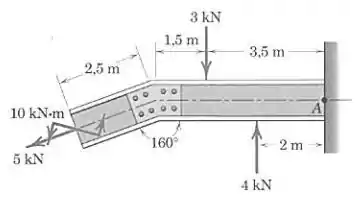
Passo 1
Observe a figura a seguir:
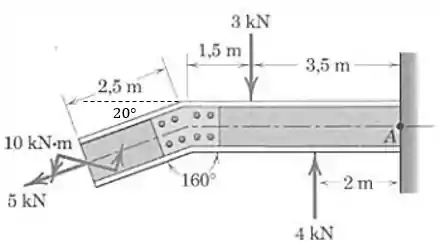
Assim, temos:
Portanto,
Passo 2
Agora, somamos o binário junto aos momentos causados por cada uma das três forças para obter o momento total :
Resposta
(sentido anti-horário)
Exercícios de Livros Relacionados
139. Determine o ângulo de projeto θ ( θ90 ° ) entre as duas barras de modo que a força horizontal de 500N tenha uma componente de 600N direcionada de A para C . Qual é a componente da força que atua
138. Determine a intensidade e a direção da resultante F x = F 1 + F 2 + F 3 das três forças encontrando primeiro a resultante F ' = F 1 + F 3 e, depois, formando F R = F ' + F 2 . Especifique sua dir
140. Determine a intensidade mínima e a direção da força F 3 de modo que a resultante de todas as três forças tenha uma intensidade de 100N .
21. Determine a intensidade de F de modo que o momento de binário resultante que age sobre a viga seja 1,5k N ⋅ m no sentido horário.
Determine o momento binário resultante que age sobre a chapa triangular.