Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas - Ex. 44
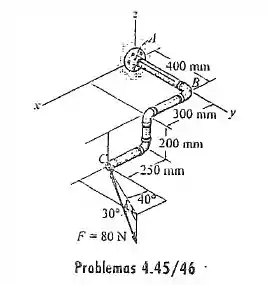
O encanamento esta sujeito á força de . Determine o momento dessa força em relação ao ponto .
Passo 1
Falaaa! Ele quer o momento causado por em relação ao ponto . A gente vai precisar escrever na forma vetorial, para achar o momento na forma vetorial também.
Para determinar o momento em seu vetor cartesiano, precisamos também determinar o vetor dito como comprimento.
Como assim vetor comprimento? Bem, ele é um vetor que começa no ponto (o ponto em relação a qual a gente quer o momento) e vai até qualquer ponto na linha de ação da nossa força. Podemos escolher o ponto , que é o ponto de aplicação da força.
Precisamos então determinar o vetor .
E ao determinar o vetor , o momento causado pela força vai ser esse produto vetorial:
Bora!
Passo 2
Determinando o vetor , Vamos lá!
Note que na figura temos os eixos cartesianos, olhando para figura, podemos afirmar que as coordenadas do ponto são as seguintes:
Multipliquei cada ponto por para converter a unidade para .
E as coordenadas do ponto , ficam o seguinte:
Considerando o ponto como inicial e o ponto como final do nosso vetor, pode ser determinado, pela seguinte definição:
Substituindo os pontos, temos:
Passo 3
Perceba que precisamos determinar as nossa força na forma cartesiana. Como o problema nos fornece os ângulos de inclinação do vetor força, podemos decompô-lo em suas componentes , e .
Para componente , temos o seguinte triângulo retângulo:
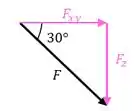
Aplicando seno:
Vamos aproveitar o desenho e iremos determinar o vetor , pois, dele iremos de compor para e .
Aplicando cosseno:
Para aos eixos e , temos outro triângulo. Decompondo o vetor , temos:
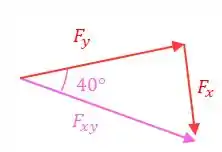
Aplicando cosseno:
Aplicando seno:
Passo 4
Executamos a decomposição do nosso vetor força e calculamos cada componente sua. Portanto, temos o vetor força como:
Nossa componente é negativo porque no desenho a força ponta para baixo.
Substituindo nossos cálculos:
Substituindo , temos:
Passo 5
Temos o vetor e a nossa força na forma cartesiana. Para obtermos o momento na forma cartesiana, basta efetuar o produto vetorial de :
Efetuando o determinante, temos: