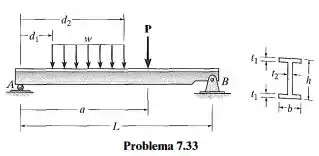
Escreva um código computacional que possa ser usado para determinar a tensão de cisalhamento máxima na viga que tem a seção transversal de mostrada na figura e é submetida a uma carga constante distribuída específica w e à força concentrada P. Mostre uma aplicação do código usando os valores

Código em MATLAB:

% Entrada de dados

L = 4; %m

a = 2; %m

P = 1.5;%kN

d1 = 0; %m

d2 = 2; %m

w = 400; %N/m

t1 = 15; %mm

t2 = 20; %mm

b = 50; %mm

h = 150; %mm

% ====== Calculando alguns termos úteis ======

% Tamanho do carregamento distribuido

dw = d2 - d1;

% ====== Calculando as reações de apoio ======

% Pelo somatorio de momentos em A

Fb = (P*a + w*dw*(d1+dw/2))/L;

% Pelo somatorio de forças em Y

Fa = w*dw + P - Fb;

% ====== Encontrando a força máxima ======

% Pelo formato do carregamento, a força máxima deve ser

% Fa ou Fb. Então basta usar o maior entre eles como

% força cortante

if Fa > Fb

V = Fa;

else

V = Fb;

end

% Convertendo a força máxima para newtons

V = V*1000;

% ====== Calculando o momento de inércia ======

I = (b*h^3)/12 -(b*(h-2*t1)^3)/12 + (t2*(h-2*t1)^3)/12; % mm^4

% ====== Calculando o momento de estático ======

% Centroides para momento estático

y_aba = h/2 + t1/2; % mm

y_alma = h/4; % mm

% Momento estático máximo

Q = t1*b*y_aba + t2*(h/2 - t1)*y_alma; % mm^3

% ====== Calculando a tensão de cisalhamento máxima ======

tensao = V*Q/(I*t2); % MPa