Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 46
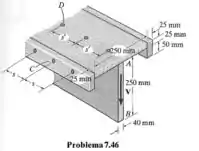
A viga é feita com quatro tábuas pregadas como mostra a figura. Se cada um dos pregos puder suportar uma força de cisalhamento de , determine os espaçamentos e exigidos entre eles se a viga for submetida a um cisalhamento
Passo 1
Fala ai galerinha do RespondeAí, tudo belezinha?
Saca só, nesse exercício aqui o enunciado nos diz que a viga é feita com quatro tábuas pregadas de acordo com a figura que ele nos fornece. Sabendo que cada prego pode suportar uma força de cisalhamento de , o enunciado nos pede para determinar os espaçamentos e necessários entre eles caso a viga seja submetida a um cisalhamento .
Belezoca, entãi primeiro fazendo os diagramas da viga, teremos:
Vamos calcular primeiro as propriedades geométricas: Centroide, Momento de Inércia.
Em segundo, vamos calcular o espaçamento dos pregos das abas, para isso vamos calcular o momento estático de uma (ou ambas) das abas e aplicar a equação de fluxo de cisalhamento.
Por fim, faremos o mesmo para o espaçamento nos pregos centrais, mas para isso vamos usar o momento estático da alma.
Passo 2
Calculamos o centroide da seção transversal:
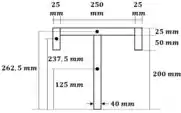
Logo:
Passo 3
Podemos calcular o momento de inércia da figura:
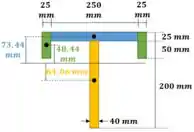
De modo que:
Sendo assim, obtemos:
Segue que o momento toal será dado como:
Passo 4
Vamos analisar primeiro a vista lateral. Vamos selecionar uma das abas para calcular o momento estático, já que primeiro queremos calcular o espaçamento dos pregos nas abas,
Passo 5
Para uma das abas, o cisalhamento do prego é simples, então o fluxo de cisalhamento sobre o prego é:
E a fórmula do fluxo de cisalhamento é:
Igualando as expressões:
Isolando o :
Passo 6
Calculamos agora o espaçamento dos pregos centrais. Pra isso precisamos do momento estático:
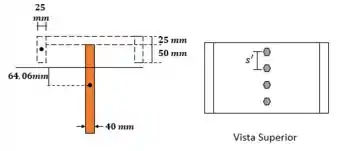
Passo 7
Podemos calcular o espaçamento de maneira similar ao feito anteriormente: