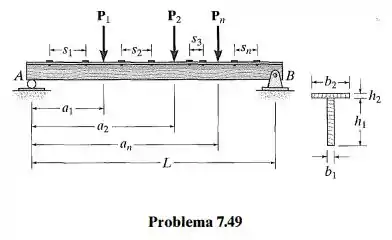
A viga de madeira T está sujeita a uma carga composta por n forças concentradas, . Se a tensão de cisalhamento admissível para cada um dos pregos for conhecida, escreva um código computacional que especifique o espaçamento dos pregos entre cada carga. Mostre uma aplicação do código usando os valores e .

Cógido em MATLAB:

% ====== Entrada de dados ======

L = 4.5; %m

a = [1.2 2.4]; %m % lista de distâncias

P = [3 7.5]; %kN % lista de carregamentos

b1 = 37.5; %mm

h1 = 250; %mm

b2 = 200; %mm

h2 = 25; %mm

V_prego = 1; %kN

% ====== Calculando as reações de apoio ======

% Pelo somatorio de momentos em A

Fb = sum(P.*a)/L; % kN

% Pelo somatorio de forças em Y

Fa = sum(P) - Fb; % kN

% ====== Encontrando a força máxima ======

% Pelo formato do carregamento, a força máxima deve ser

% Fa ou Fb. Então basta usar o maior entre eles como

% força cortante

if Fa > Fb

V = Fa;

else

V = Fb;

end

% ====== Calculando o centroide da seção ======

y_alma = h1/2; %mm

y_aba = h1 + h2/2; %mm

yc = (b1*h1*y_alma + b2*h2*y_aba) / (b1*h1 + b2*h2); %mm

% Distancia entre os centroides e o centroide da seção

d_y_alma = yc - y_alma; % mm

d_y_aba = y_aba - yc; % mm

% ====== Calculando o momento de inércia ======

I_alma = (b1*h1^3)/12 + b1*h1*(d_y_alma)^2; % mm^4

I_aba = (b2*h2^3)/12 + b2*h2*(d_y_aba)^2; % mm^4

I = I_alma + I_aba; % mm^4

% ====== Calculando o momento de estático ======

% Vamos calcular o momento estático da aba

Q_aba = b2*h2*d_y_alma; % mm^3

% ====== Calculando o fluxo de cisalhamento máxima ======

q = V*Q_aba/I; % kN/mm

% ====== Calculand o espaçamento ======

s = V_prego/q;