Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 3

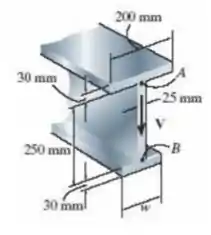
Se a viga de abas largas for submetida a um cisalhamento V = 30 kN, determine a força de cisalhamento à qual a alma da viga resiste. Considere w = 200 mm.

Passo 1

Falaaa galerinha bonita, tudo belezinha com vocês?

Saca só, o enunciado nos diz que se a viga de abas largas for submetida a um cisalhamento V = 30   kN , então sabendo que w = 200   mm , o enunciado pede pra gente determinar a força de cisalhamento à qual a alma da viga resiste.

Belezoca, como a peça é simétrica sabemos que o centroide fica bem no meio dela.

Dito isto, vamos calcular o momento de inércia total da peça:

I = 2 0,2 × 0,03 3 12 + 0,2 × 0,03 × 0,140 2 + 0,025 × 0,25 2 12

I = 2,68652 × 10 - 4   m 4

Passo 2

Iradoso, agora sabemos que Q e τ variam em função de y .

Assim, devemos obter o momento estático, porém deixando-o em função de y (distância até a base da peça):

Q y = ∑ y C G ' A

Logo:

Q y = 0,14 0,2 × 0 , 0 3 + y + 0,125 - y 2 0,025 0,125 - y

Q y = 1,0353 - 12,5 y 2 10 - 3   m³

Passo 3

Assim podemos obter τ ( y ) : a tensão cisalhante em função de y , dada como:

τ y = V Q y I t

Logo:

τ y = 30 × 10 3 1,0353 - 12,5 y 2 10 - 3   2,68652 × 10 - 4 0,025

τ y = 4,624 - 55,834 y 2

Show de bolinhas, então agora a gente pode distribuir a função da tensão acima pela área da alma, integrando para obter V a l m a , tal que:

V a l m a = ∫ a l m a   τ d A

Segue que:

V a l m a = ∫ - 0,125 0,125 4,624 - 55,834 y 2 10 6 0,025   d y

V a l m a = 27,1   kN

Resposta

V a l m a = 27,1 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma chapa de aço com espessura 6 mm é dobrada para formar a seção de paredes finas mostrada na figura. Se for submetida a uma força de cisalhamento V = 1,25 kN, determine a tensão de cisalhamento nos
A viga é composta por quatro tábuas coladas ao longo das linhas de junção. Se a cola puder resistir a 15 kN/m e a viga sofrer uma rotação de 90°, qual é o cisalhamento vertical máximo V que a viga pod
A viga é composta por quatro tábuas coladas ao longo das linhas de junção. Se a cola puder resistir a 15 kN/m, qual é o cisalhamento vertical máximo V que a viga pode suportar?
O elemento está sujeito a uma força de cisalhamento V = 2 kN. Determine o fluxo de cisalhamento máximo no elemento. Todos os segmentos da seção transversal têm 15 mm de espessura.
Uma chapa de aço com espessura 6 mm é dobrada para formar a seção de paredes finas mostrada na figura. Se for submetida a uma força de cisalhamento V = 1,25 kN, determine a tensão de cisalhamento no p