Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 67
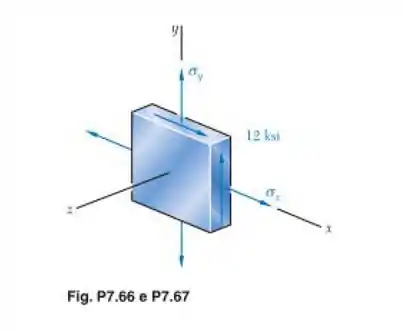
Para o estado plano de tensão mostrado na figura, determine a tensão de cisalhamento máxima quando (a) e e (b) e . (Sugestão: Considere as tensões de cisalhamento no plano e fora do plano das tensões.)
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Nesse exercício, para determinar a tensão de cisalhamento máxima, nós precisamos saber se as tensões máxima e mínima possuem o mesmo sinal ou se possuem sinais opostos. Se possuírem sinais opostos, sabemos que a tensão de cisalhamento máxima será o próprio raio do círculo de Mohr. Se possuírem o mesmo sinal, sabemos que a tensão de cisalhamento máxima será metade da tensão normal máxima.
Então já deu pra perceber que vamos precisar de algumas informações referentes ao círculo de Mohr né, vamos precisar da tensão média, do raio do círculo e das tensões máxima e mínima. Então bora lá!
Passo 2
Vamos começar o exercício com os dados da letra (a), onde temos:
Beleza! Com essas informações já podemos calcular a tensão média, que será dada por:
Agora, podemos utilizar a fórmula para o raio do círculo de Mohr, dada por:
Substituindo os valores conhecidos, chegamos em:
Beleza, com a tensão média e o raio do círculo, podemos calcular os valores da tensão máxima e mínima, que serão dados por:
Opa! Os sinais da tensão máxima e mínima são iguais, então isso quer dizer que a tensão de cisalhamento máxima será metade da tensão máxima, ou seja:
Passo 3
Agora vamos para a letra (b), onde temos os seguintes valores para a tensão:
Beleza! Com essas informações já podemos calcular a tensão média, que será dada por:
Agora, podemos utilizar a fórmula para o raio do círculo de Mohr, dada por:
Substituindo os valores conhecidos, chegamos em:
Beleza, com a tensão média e o raio do círculo, podemos calcular os valores da tensão máxima e mínima, que serão dados por:
Opa! Os sinais da tensão máxima e mínima são opostos, então isso quer dizer que a tensão de cisalhamento máxima será o próprio raio do círculo, ou seja:
Feshooow! Valeu por mais uma!