Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 64
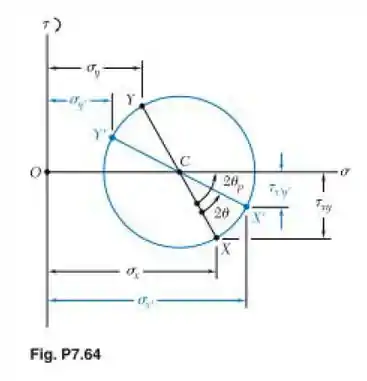
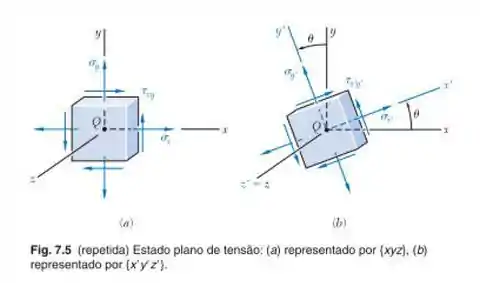
O círculo de Mohr mostrado corresponde ao estado de tensão dado nas Figs. 7.5a e b. Notando que = OC + (CX’) e que , determine as expressões para e dadas nas Equações (7.5) e (7.6), respectivamente. [Sugestão: Use sem (A+B) = senA cosB + cosA senB e cos(A+B) = cosA cosB – senA senB.]
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Vamos começar esse exercício relembrando quais são as equações 7.5 e 7.6 vistas nesse capítulo, pois são nelas que devemos chegar. Fazendo isso, vamos usar as relações trigonométricas fornecidas para desenvolver as equações e poder chegar nessas expressões.
Passo 2
Vamos começar escrevendo as equações 7.5 e 7.6 que devemos encontrar, então são elas:
Beleza! Agora nós vamos começar pela equação da tensão. Então, conforme o enunciado nos disse, temos a seguinte relação:
Então, abrindo essa relação através da relação trigonométrica sugerida no enunciado, teremos:
Agora, precisamos encontrar expressões para esses 3 termos. Começando por OC, esse ficou fácil, olhando para o círculo de Mohr, temos que será o , que é dado por:
Beleza, agora, devemos notar que CX e CX’ são iguais, já que representam o raio do círculo, então temos:
E, podemos ver que:
E, da mesma forma, com o seno, teremos a própria tensão de cisalhamento, ou seja:
Agora, substituindo as relações encontradas na equação que tínhamos para teremos:
Opaa! Essa é exatamente a equação 7.5 que queríamos encontrar. Agora bora encontrar a 7.6.
Passo 3
Agora, para a equação 7.6, temos a seguinte relação dada no enunciado:
Agora, vamos abrir essa diferença do seno utilizando a relação fornecida no enunciado, chegando em:
Lembra das relações lá do passo 2? Então, vamos usar elas de novo aqui, chegando em:
Tá aí, essa é a equação 7.6 que queríamos encontrar.