Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 79
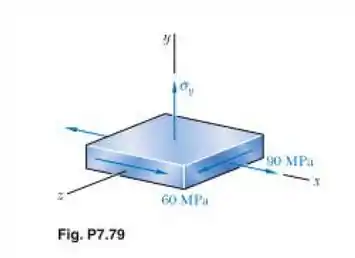
Para o estado de tensão indicado, determine dois valores de para os quais a tensão de cisalhamento máxima é de 80 MPa.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para esse exercício, nós vamos precisar desenhar o círculo de Mohr para poder analisar os extremos do círculo e encontrar a tensão supondo que ela seja a máxima e a mínina nesses pontos.
Então, para desenhar o círculo de Mohr, precisamos da tensão média e do raio do círculo, então bora lá!
Passo 2
Vamos começar escrevendo as tensões fornecidas no elemento diferencial, que são:
Beleza! Com essas informações já podemos calcular a tensão média, que será dada por:
Agora, podemos utilizar a fórmula para o raio do círculo de Mohr, dada por:
Substituindo os valores conhecidos, chegamos em:
Com isso podemos desenhar o círculo de Mohr, que será dado por:
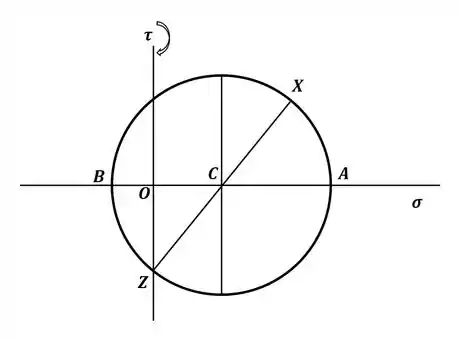
Beleza, com a tensão média e o raio do círculo, podemos calcular os valores da tensão máxima e mínima, que serão dados por:
Passo 3
Agora, com o círculo desenhado, podemos encontrar a tensão normal no ponto A, que será a tensão máxima, dada por:
E, a tensão mínima, no ponto B, será:
Agora, vamos encontrar quando ela for a tensão mínima, ou seja:
Só que nós sabemos que o pode ser dado por:
Só que, sabemos que nesse caso o raio do círculo será a própria tensão de cisalhamento dada no enunciado, então a nossa equação para será:
Substituindo os valores conhecidos, chegamos em:
Passo 4
Agora, vamos encontrar quando ela for a tensão máxima, ou seja:
Só que nós sabemos que o pode ser dado por:
Só que, sabemos que nesse caso o raio do círculo será a própria tensão de cisalhamento dada no enunciado, então a nossa equação para será:
Substituindo os valores conhecidos, chegamos em:
Feshooow! Esse é o nosso segundo valor de .