Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 94
A estrutura de um telhado consiste em madeira compensada e material de forração suportados por várias vigas de madeira de comprimento A carga permanente suportada por cada viga, incluindo seu peso estimado, pode ser representada por uma força uniformemente distribuída . O peso externo consiste em uma carga de neve, representada por uma força uniformemente distribuída e uma força concentrada de aplicada ao ponto médio de cada viga. Sabendo que o limite de resistência da madeira utilizada é e que a largura da viga é , determine a altura mínima admissível das vigas, usando com coeficientes de carga , e o coeficiente de resistência
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora estudar mecânica e garantir aquele notão na prova.
Primeiro, vamos dividir a nossa viga em 2. Na primeira, dada pelo seu peso estimado, vamos esboçar DCL:
Em seguida, vamos utilizar as equações de equilíbrio. Sabemos que:
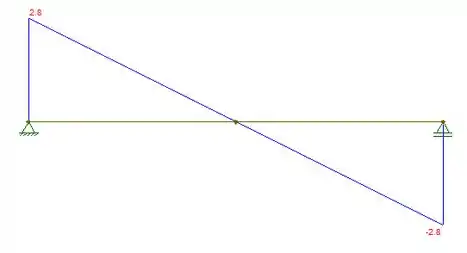
Por simetria, . Com isso, podemos esboçar o diagrama de força cortante. Fazendo ele:
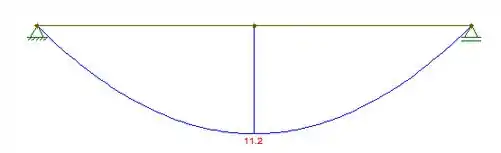
E também, o diagrama de momento:
Passo 2
Agora que encontramos os diagramas para o peso, vamos repetir o processo para a carga de neve. Vamos esboçar o DCL:
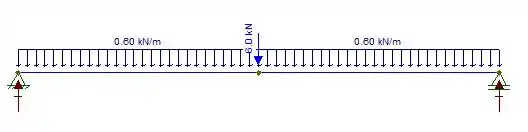
Pelas equações de equilíbrio, temos:
Assim, podemos esboçar os diagramas de força cortante e momento fletor. Eles são dados, respectivamente, por:
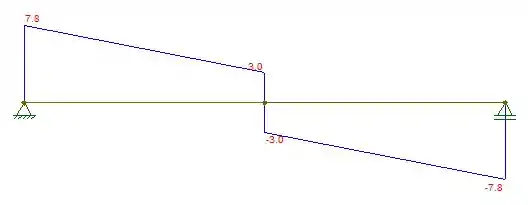
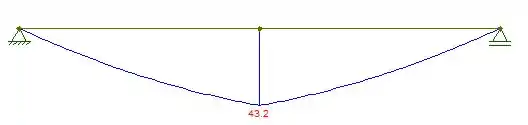
Passo 3
Por fim, para encontrarmos a altura , temos a seguinte relação para os coeficientes de carga e de resistência pelo método do :
Com isso, precisamos encontrar os momentos para os dois casos que separamos anteriormente. Para o primeiro, temos:
E para o segundo, temos:
Substituindo:
E então, podemos escrever o módulo de resistência à flexão da sessão mínima admissível para uma sessão retangular assim:
Opa, essa é a altura mínima admissível.