Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 125
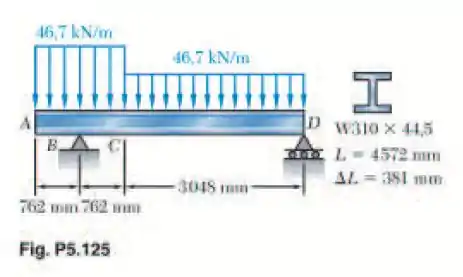
Para a viga e o carregamento mostrados, e usando um computador e funções degrau, (a) organize uma tabela de força cortante, momento fletor e tensão normal máxima em seções da viga de a , usando os incrementos indicados e (b) usando incrementos menores, se necessário, determine com 2% de precisão a tensão normal máxima na viga. Coloque a origem do eixo x na extremidade A da viga.
Passo 1
Beleza! A primeira coisa que vamos fazer é desenhar o diagrama de corpo livre para a viga, dessa forma, o DCL será:
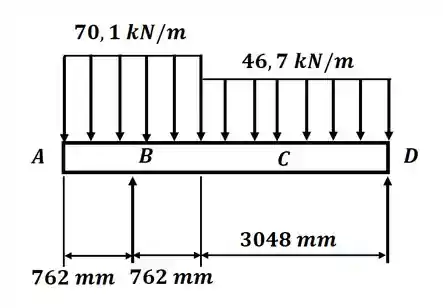
Observe que o enunciado fornece dois carregamentos com alturas diferentes, mas com valores iguais, o que não faz sentido né?! Na verdade, o valor do primeiro carregamento é de 70,1 kN/m, segundo a edição com as unidades americanas. Então, com o DCL acima, podemos aplicar o somatório de momentos em relação ao ponto D e com isso encontrar a reação no ponto B. Então teremos:
Agora, lembrando que, como temos carregamento distribuído que não vai até o final da viga, devemos adicionar um outro carregamento, de mesma intensidade, mas sentido oposto, da posição em que o carregamento atual termina, até o final da viga. Além de prolongar o carregamento existente até o final da viga também, sempre deixando o carregamento equivalente ao carregamento original. Sendo assim, o carregamento equivalente será:
Agora podemos escrever o carregamento distribuído, considerando o ponto A como origem do nosso sistema, teremos:
Passo 2
Agora podemos encontrar a força cortante sabendo que ela será o oposto da integral da equação do carregamento, ou seja:
Substituindo a expressão para e resolvendo a integral, chegamos em:
A constante de integração nesse caso corresponde as forças localizadas aplicadas no sistema, no nosso caso, temos a força de apoio em B, então nossa constante será:
Então, nossa equação para a força cortante será:
Passo 3
Agora, para encontrarmos a equação do momento fletor, como já temos a equação para a força cortante, basta lembrar que a derivada do momento equivale a força cortante, ou seja:
Isolando as variáveis dessa equação, temos:
Integrando essa expressão dos dois lados, teremos:
Agora, substituindo a expressão encontrada para no passo 1, a equação acima se torna:
Resolvendo a integral, teremos:
Em que é a constante de integração. Nesse caso, a constante de integração corresponde aos momentos localizados que são aplicados ao sistema, no nosso caso não temos nenhum momento localizado, então teremos:
Então a equação do momento será:
Passo 4
Beleza! Nós sabemos que a tensão normal máxima provocada pelo momento fletor é dada por:
No nosso caso, temos uma viga W310 X 44,5. Então devemos ir lá apêndice C pegar as suas propriedades, vamos precisar do momento de inércia e da altura total da viga, então teremos
Sabemos que a distância para obter a tensão máxima será metade da altura da viga, pois as maiores tensões estarão na extremidade. Então teremos:
Dessa forma, substituindo os valores conhecidos, nossa tensão máxima será dada por:
Então, agora temos todas as equações que precisamos, de força cortante, momento fletor e da tensão máxima. Agora, com o auxílio do computador, calculando o valor da força cortante e do momento fletor em cada um dos pontos, começando de com incremento de , e calculando também a tensão máxima em cada um desses pontos, teremos a seguinte tabela de valores:
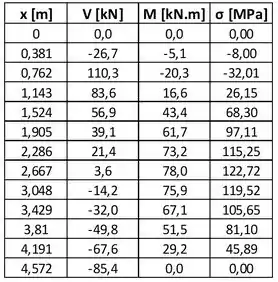
Opa! A letra (a) acabou aqui! Bora pra letra (b) agora!
Passo 5
Agora, para a letra (b), devemos encontrar a tensão normal máxima da viga, com uma precisão de 2%. Para isso, primeiro vamos olhar a tabela que valores que encontramos no passo 4. Lá podemos ver que o maior valor de tensão encontrado foi de:
E na posição:
Podemos ver que antes desse ponto, tínhamos:
E após, temos:
Podemos ver na tabela que nesses 3 valores, temos a tensão de cisalhamento mudando de sinal entre e . E nós sabemos que quando temos cisalhamento igual a zero, isso implica em um ponto máximo de momento, pois a equação do cisalhamento é a derivada do momento. Dessa forma, sabemos que o valor máximo está entre esse intervalo de comprimento, então, calculando os valores de tensão dentro desse intervalo, chegamos numa tensão máxima de: