Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 118

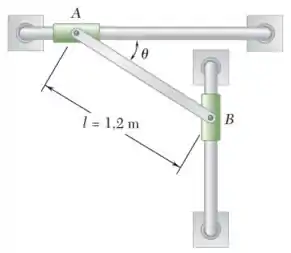
As extremidades da haste uniforme AB de 10 kg são presas a cursores de peso desprezível que deslizam sem atrito ao longo de hastes fixas. Uma força vertical P é aplicada ao cursor B quando θ = 25°, fazendo o cursor partir do repouso com uma aceleração para cima de 12 m/s2 . Determine (a) a força P, (b) a reação em A.

Passo 1

O exercício pede que a gente determine (a) a força P, (b) a reação em A.

Cinematica: ω = 0

a B = a A + a B / A ; 12 m / s 2 ↑ = a A ← + 1.2 α   ∀   25 ∘ a B = a B / A c o s ⁡ 25 ∘

α = 11.034 r a d / s 2 a A = 12 t a n ⁡ 25 ∘ = 5.596 m / s 2 ← a G = a A + a G l A : a G = [ 5.596 ← ] + 0.6 α   ∀   25 ∘

a G = [ 5.596 ← ] + 0.6 11.034   ∀   25 ∘ a ¯ x = a G x = 2.798 m / s 2 ← a ¯ y = a G y = 6.00 m / s 2 ↑

Passo 2

Cinética

I → = 1 12 m L 2 = 1 12 m ( 1.2 ) 2

(a)

+ ) Σ M E = Σ M K e f f : P ( 1.0876 ) - W ( 0.5438 ) = I - α + m a - x ( 0.2535 ) + m a - y ( 0.5438 ) W = m g = 10 ( 9.81 ) = 98.1 N I - α = 1 12 m L 2 α = 1 12 ( 10 ) ( 1.2 ) 2 ( 11.034 ) = 13.24 N ⋅ m m a - x = ( 10 ) ( 2.798 ) = 27.98 N m a - y = ( 10 ) ( 6 ) = 60 N P ( 1.0876 ) - ( 98.1 ) ( 0.5438 ) = 13.24 + ( 27.98 ) ( 0.2535 ) + ( 60 ) ( 0.5438 ) P ( 1.0876 ) - 53.347 = 13.24 + 7.096 + 32.628 P ( 1.0876 ) = 106.311 P = 97.8 N

Passo 3

(b)

+ ∣ Σ F y = Σ F y e f f : A - W + P = m a - y A - 98.1 + 97.8 = 60 N

Resposta

( a ) P = 97.8 N ↑

b B = 60 .   3 N ↑

Ver Outros Exercícios desse livro