Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 3
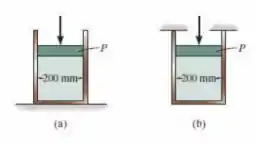
A figura mostra duas alternativas para apoiar o cilindro de parede fina. Determine o estado de tensão na parede do cilindro para ambas as alternativas, se o pistão P provocar uma pressão interna de 0,5 MPa. A parede tem espessura de 6 mm, e o diâmetro interno do cilindro é 200 mm.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora.
Bom, nosso enunciado nos diz que o nosso reservatório é cilíndrico e tem um pistão que gera uma pressão de 0,5MPa e que tem paredes com 6mm de espessura e 100 mm de raio interno.
Depois de falar isso tudo, ele nos pede o estado de tensão nos dois casos: quando está apoiado no chão (caso A) e quando está pendurado no teto (caso B).
Bora lá fazer?? Partiu??
Passo 2
Nas questões de vasos cilíndricos de paredes finas, temos duas tensões normais: (na direção circunferencial, ou seja, do aro) e(no sentido longitudinal, ou seja, axial).
No caso A, como o vaso está apoiado no chão, não temos a tensão axial. Por que? Nesse caso, as reações à força no pistão são produzidas pelo chão, sem causar tração nas paredes. Os esforços são transmitidos pelo fluído dentro do cilindro e são resistidos pelo chão.
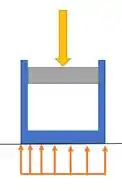
Aí não temos tensões na direção longitudinal nas nossas paredes. Mas teremos na direção circunferencial.
Já no caso , há tração nas laterais, porque os esforços que seguram o cilindro no teto passam pelas laterais no sentido longitudinal.
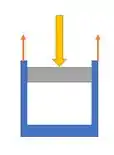
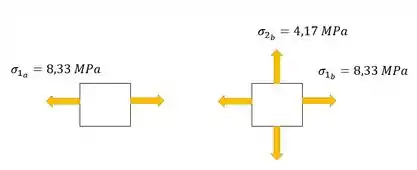
Disso, podemos concluir que as nossas tensões para cada caso serão:
Caso A -
Caso B - e
Passo 3
Aí para achar essas tensões, usamos as duas respectivas fórmulinhas:
Onde, para os dois casos:
Onde é a pressão, é o raio interno e a textura da parede.
Ficamos então, com:
E para :
Os estados de tensões ficam:
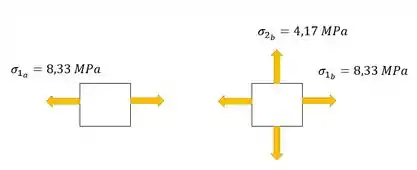
Obs: aqui ficamos diferente do gabarito por uma questão de erro de tradução do livro, tá bem?
Resposta
