Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 54
O elemento consiste em dois canais U de plástico com 12 mm de espessura colados em A e B. Se a cola puder suportar uma tensão de cisalhamento admissível de , determine a intensidade máxima de do carregamento distribuído triangular que pode ser aplicado ao elemento tomado como base a resistência da cola
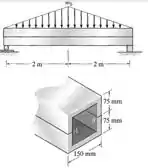
Passo 1
Faaala aí!
Esses são os dados da questão:
A questão pede o maior carregamento possível na viga:
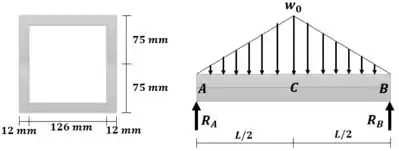
Estratégia de resolução: Primeiro vamos calcular as reações de apoio, e determinar o ponto onde o esforço interno é máximo.
Depois calculamos o momento de inércia e o momento estático da região de interesse. Como a seção é perfeitamente simétrica, não é preciso calcular o centroide.
Por fim, usamos a equação de tensão de cisalhamento para calcular o carregamento máximo sobre a viga.
Vem ver como fica!
Passo 2
Como o carregamento é perfeitamente simétrico, sabemos que:
Aplicando a equação de equilíbrio:
Passo 3
Agora calculamos o gráfico de esforço cortante utilizando o método gráfico
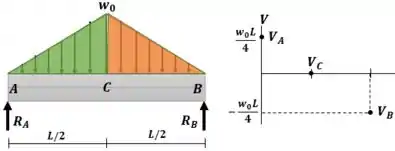
A gente vai calcular os valores do cortante nos pontos e .
Como nosso carregamento é linear em e em , o diagrama precisa estar num grau a mais, então ele precisa ser uma parábola em e em . Aí então ligamos esses pontos que a gente achou por parábolas.
O gráfico resultante é:
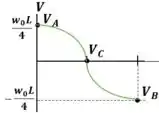
A maior força interna ocorre no ponto A
Passo 4
Agora vamos calcular o momento de inércia de toda a figura. Para isso basta calcular como se a estrutura fosse maciça e depois subtrair o valor da região vazada:
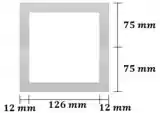
Passo 5
Agora vamos calcular o momento estático de uma região que tenha contato com a cola. A região escolhida está em destaque abaixo.
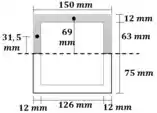
Para escolher a região de cê pode imaginar assim: eu quero ver o cisalhamento na região da cola. Se eu segurar uma das metades da seção e tirar a cola, que parte da seção fica na minha mão? Se você segurou em cima, seria a parte sombreada né?
Aí a gente precisa calcular o centroide dessa região.
Passo 6
A tensão na região da cola é:
Repara que a gente usou porque temos dois lugares de espessura em contanto com a outra metade da seção através da cola.
Isolando
Substituindo os valores:
Prontinho!
Obs: O gabarito nessa está com um errinho, beleza?