Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 22
A força vertical P age na parte inferior da capa cujo peso é desprezível. Determine a distância máxima até a borda na qual aquela força pode ser aplicada de modo a não produzir nenhuma tensão de compressão na seção da chapa. A chata tem espessura de 10mm, e age ao longo da linha central dessa espessura.
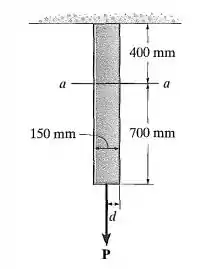
Passo 1
Primeiro, vamos fazer o DCL:
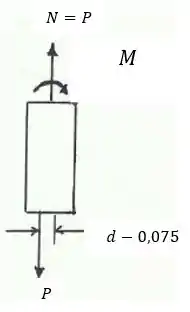
Passo 2
Com isso, vamos calcular o momento e equilíbrio:
Passo 3
Em seguida, vamos calcular a tensão:
Para que a tensão de compressão seja nula , temos:
=0
Resposta
Exercícios de Livros Relacionados
Dois elementos de madeira de seção transversal retangular uniforme de 80 × 120m m são unidos por uma junta colada conforme mostra a figura. Sabendo que β = 22 ° e que as tensões máximas admissíveis na
Dois elementos de seção transversal uniforme de 50 m m × 80 m m são colados entre si ao longo do plano a - a , que forma um ângulo de 25 ° com a horizontal. Sabendo que as tensões admissíveis para a j
O eixo de um automóvel está sob a ação das forças e torque mostrados na figura. Sabendo que o diâmetro do eixo de seção transversal cheia é de 32 m m , determine (a) os planos e tensões principais no
Uma força vertical de 400l b é aplicada em D em uma engrenagem fixada ao eixo sólido A B de 1i n de diâmetro. Determine as tensões principais e a tensão de cisalhamento máxima no ponto H localizado no
A força P centrada é aplicada a um pilar curto conforme mostrado. Sabendo que as tensões no plano a - a são σ = - 15k s i e τ = 5k s i , determine (a) o ânguloβ que o plano a - a forma com a horizonta