Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 58
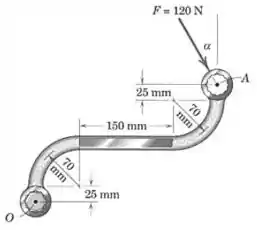
A força de é aplicada em uma extremidade da chave curva, como mostrado. Se , calcule o momento de em relação ao centro do parafuso. Determine o valor de que maximizaria o momento em relação a . Dê o valor deste momento máximo.
Passo 1
Já que temos o valor do ângulo , podemos começar decompondo a força e calculando o momento em relação a cada uma das componentes.
Começamos pela componente de na direçao vertical:
Qual é a distância entre a linha de ação dessa força e o ponto ?
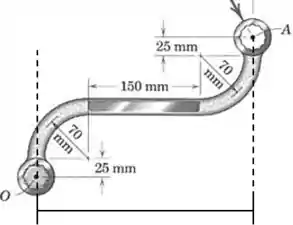
Podemos somar os diversos trechos para encontrar essa distância:
Então o momento dessa componente é:
Passo 2
Agora podemos usar a mesma lógica para calcular o momento da outra componente da força:
E dessa vez temos que olhar para a distância “vertical” entre a linha de ação dessa força e o ponto .
E então o momento é:
E então o momento total da força é:
Passo 3
Agora queremos encontrar o valor de que maximiza o momento. Esse é necessariamente o ângulo que deixa a força na direção perpendicular à reta queu une e :
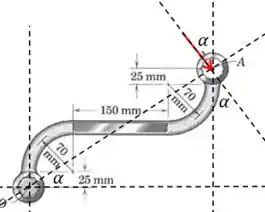
E só temos que lidar com as distâncias que já calculamos nos passos anteriores:
E podemos calcular o momento da força nesse caso usando a mesma fórmula de antes:
Resposta
O momento da força é , o ângulo que maximiza o momento é e nesse caso teríamos .