Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 45

Ao se levantar o poste a partir da posição mostrada, a força trativa T no cabo deve gerar um momento de 72   k N ∙ m em torno de O . Determine T .

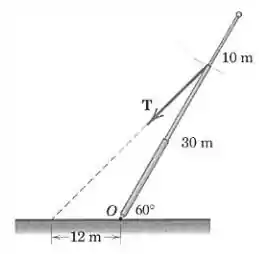
Passo 1

Galera, a força T faz um ângulo α com o poste, conforme mostra a figura:

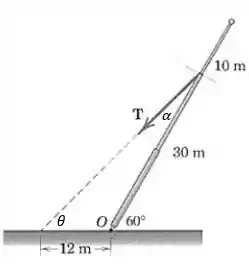
Podemos usar a lei dos senos no triângulo para tentar determinar o ângulo α :

s e n   α 12 = s e n   θ 30

2,5   s e n   α = s e n   θ

Mas a gente consegue obter o ângulo θ em função de α , fazendo a soma dos ângulos de um triângulo:

α + θ + 180 ° - 60 ° = 180 °

θ = 60 ° - α

Passo 2

Voltando à equação, usamos a fórmula do seno da subtração de dois ângulos:

2,5   s e n   α = s e n   θ = s e n 60 ° - α

2,5   s e n   α = s e n   60 ° cos ⁡ α - s e n   α cos ⁡ 60 °

E agora dividimos toda a equação por cos ⁡ α :

2,5   t g   α = s e n   60 ° - t g   α cos ⁡ 60 °

Isolamos t g   α :

t g   α = s e n   60 ° 2,5 + cos ⁡ 60 °

t g   α = 0,28868

Por fim,

α = t g - 1 0,28868

α = 16,102 °

Passo 3

Show! Agora é só lembrar que o momento de uma força T em torno de O pode ser dado pela fórmula:

M O = T r   s e n   α

onde r é a distância entre o ponto de aplicação da força e o ponto O . Ou seja,

72   k N ∙ m = T   30   m   s e n   16,102 °

T = 8,65   k N

Resposta

T = 8,65   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sérios danos ao pescoço podem ocorrer quando um jogador de futebol americano é atingido na proteção de rosto de seu capacete da maneira mostrada, causando um mecanismo de guilhotina. Determine o momen
Determine o momento da força F em relação ao ponto A como uma função de θ . Represente os resultados de M (ordenada) em função de θ (abscissa) para ( 0 ° ≤ θ ≤ 180 ° ) .
Determine o ângulo θ ( 0 ° ≤ θ ≤ 180 ° ) da força F de modo que ela produza um momento máximo e um momento mínimo em relação ao ponto A . Além disso, quais são as intensidades desses momentos máximo e
Determine o momento produzido pela força F em relação ao ponto A em função do ângulo θ . Construa o gráfico de M A em função de θ , onde ( 0 ° ≤ θ ≤ 180 ° ) .
A barra no mecanismo de controle de potência de um jato comercial esta sujeita a uma força de 80N . Determine o momento dessa fora em relação ao mancal em A .