Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 44

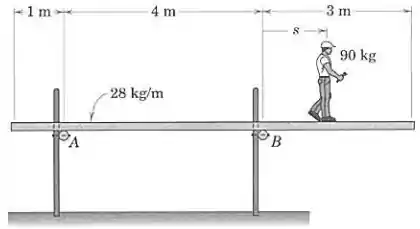
A plataforma uniforme, que tem uma massa por unidade de comprimento de 28   k g / m , está simplesmente apoiada sobre barras de apoio em A e em B . Um trabalhador de construção civil com 90   k g sai do ponto B e anda para a direita. Em que posição s o momento combinado do peso do homem e da plataforma será zero em relação a B ?

Passo 1

Galera, vamos chamar de M B H o momento do peso do homem, e de M B P o momento do peso da plataforma, ambos em relação a B . Então, o momento combinado M B dessas duas forças será:

M B = M B H + M B P

Note que o peso P H do homem tem tendência a fazer girar no sentido horário (negativo), atuando a uma distância s de B . Então o momento dessa força será:

M B H = - P H s = - m H g s = - 90 9,81 s

M B H = - 882,9 s   N ∙ m

Passo 2

Como temos apenas a densidade linear da plataforma, μ = 28   k g / m , precisamos do seu comprimento L para calcular o peso P P da plataforma. De acordo com a figura, temos:

L = 1 + 4 + 3 = 8   m

Portanto,

P P = m P g = μ L g = 28 8 9,81 = 2197,4

Essa força vai atuar no ponto médio da plataforma, já que ela é uniforme. Esse ponto médio x - é calculado dessa maneira:

x - = L 2 = 8 2 = 4   m

Assim, a força P P atuará para baixo à esquerda do ponto B , causando uma tendência de giro no sentido anti-horário (positivo). A distância d desse ponto médio até o ponto B será:

d = x - - 3 = 4 - 3 = 1   m

Logo, o momento dessa força será:

M B P = + P P d = 2197,4 1 = 2197,4   N ∙ m

Passo 3

Queremos que o momento combinado do peso do homem e da plataforma será zero em relação a B , ou seja:

M B = 0

M B H + M B P = 0

Vamos substituir os valores que encontramos para cada um desses momentos, a fim de determinar a posição s , em metros, para que isso ocorra:

- 882,9 s + 2197,4 = 0

s = 2197,4 882,9

s = 2,49   m

Resposta

s = 2,49   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

30. Se F B = 150N e F C = 225N , determine o momento resultante em relação ao parafuso localizado em A.
32. O cabo de reboque exerce uma força P = 4k N na extremidade da lança do guindaste de 20 m de comprimento. Se θ = 30 ° , determine o posicionamento x do gancho em A para que essa força crie um momen
28. A força de 70N age na extremidade do tubo em B. Determine os ângulos θ ( 0 ° ≤ θ ≤ 180 ° ) da força que produzirá os momentos máximo e mínimo em relação ao ponto A. Quais são as intensidades desse
A fim de erguer o poste de iluminação a partir da posição mostrada, a força F no cabo deve ciar um momento de 2250N ∙ m no sentido anti-horário em relação ao ponto A . Determine a intensidade de F que
A fim de erguer o poste de iluminação a partir da posição mostrada, a força F é aplicada ao cabo. Se F = 1000N , determine o momento produzido por F em relação ao ponto A .