Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 56
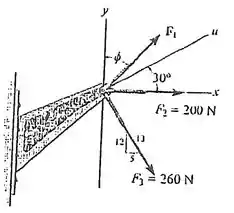
Se a força resultante que atua sobre o suporte precisa ser mínima, determine as intensidades de e da força resultante. Considere .
Passo 1
Queremos a força resultante mínima, lembra de máximos e mínimos? Sim, vamos usar derivada, fica tranquilo que é facinho.
Antes vamos achar o ângulo que faz com x, como a informação dele é dada através de um triângulo vamos achar por:
Agora, vamos começar fazendo o somatório das forças nos eixos.
Em x:
Em y:
Passo 2
Vamos agora achar o módulo da nossa força resultante:
Nossa força resultante está em função de , se derivarmos a e igualarmos a 0 descobriremos nos pontos de máximo ou mínimo:
Igualando a 0:
Passo 3
Por fim, podemos achar nossa substituindo na equação do módulo:
Resposta
Exercícios de Livros Relacionados
Determine a intensidade da força resultante F R e sua direção, medida em sentido horário a partir do eixo u positivo.
Uma pequena sonda P é levemente forçada contra uma superfície circular com uma força F , como mostrado. Determine as componentes n e t desta força como função da posição horizontal s .
A força F de 1800N é aplicada à extremidade da viga em I. Expresse F como um vetor, usando os vetores unitários i e j .