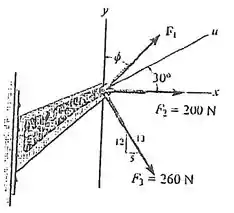
Se a intensidade da força resultante que atua sobre o suporte deve ser direcionada ao longo do eixo positivo, determine a intensidade de e sua direção .

Nesse exercício nos é dada a força resultante e queremos a , mas para achar é tudo farinha do mesmo saco, só que agora vamos usar outro eixo, sabemos que:

Como teremos uma força resultante em , forças perpendiculares a devem se anular, que seria digamos o “” do nosso eixo, vamos chamar de :

Perceba que a orientação de é dada por um triângulo, e sua direção em relação a será . O ângulo do triângulo encontramos pelo:

Ficando nosso ângulo de com :

Já que ele passa dos , vou considerar a força no sentido oposto e com ângulo de . Assim, a componente de em será:

Já nosso faz um ângulo com , assim, a força atuante no eixo :

Agora para o eixo que já nos referimos: